«состав числа 4» нод в подготовительной к школе группе

Числа от 1 до 100. Состав числа. Круглые числа

Предыдущее и последующее число

Предыдущее число — то число, которое при счете следует перед данным числом.

56, 57

Последующее число — то число, которое при счете называют сразу после данного числа.

56, 57

Однозначные и двузначные числа

Вспомни, что каждая цифра в записи занимает определенное место.

Единицы стоят на первом месте справа.

Десятки стоят на втором месте справа.

Однозначные числа записываются ОДНОЙ цифрой: 5, 9, 2, 5.

Двузначные числа записываются ДВУМЯ цифрами: 54, 91, 42, 85.

Самое маленькое однозначное число — .

Самое большое однозначное число — 9.

Самое маленькое двузначное число — 10.

Самое большое двузначное число — 99.

Состав двузначного числа

Всего на рисунке 35 палочкек.

35 = 3 дес. 5 ед.

35 = 30 + 5

Состав числа 35 — 3 дес. 5 ед.

Красных палочек 12.

12 = 1 дес. 2 ед.

12 = 10 + 2

Состав числа 12 — 1 дес. 2 ед.

Синих палочек всего 23.

23 = 2 дес. 3 ед.

23 = 20 + 3

Состав числа 23 — 2 дес. 3 ед.

Теперь научимся представлять числа в виде суммы разрядных слагаемых.

Какие разряды выделяют в двузначных числах?

В двузначных числах выделяют разряд десятков и разряд единиц, то есть двузначное число можно представить следующим образом:

десятки + единицы

В числе 35 три десятка и 9 единиц:

35 = 30 + 5

Сравнение двузначных чисел

Числа 42 и 24 похожи тем, что в их записи использованы одинаковые цифры: цифра 4 и цифра 2. Но цифра 4 для числа 42 означает десятки, а для 24 — единицы, цифра 2 для числа 42 означает единицы, а для 24 — десятки.

Число	42	24
Количество десятков	4	2
Количество единиц	2	4

42 > 24

1. Сравнение двузначных чисел всегда начинается с десятков.

2. Если количество десятков одинаково, тогда переходят к сравнению единиц.

Круглые числа

Числа, которые оканчиваются на 0, называются круглыми. — 60, 30, 20.

или

В разряде единиц у круглого числа — число 0. — 70, 90, 40.

10, 20, 30, 40, 50, 60, 70, 80, 90, 100.

10 + 40 = ?

1 дес. + 4 дес. = 5 дес.

5 дес. = 50, значит,

10 + 40 = 50

Десять любых предметов можно назвать – ОДИН ДЕСЯТОК.

Десятками можно считать:

— это 2 десятка — записываю так: 2 дес.

Действия с десятками и единицами

— это 31

Как решить пример 34 + 25?

34 — это 3 дес. и 4 ед.

25 — это 2 дес. и 5 ед.

3 дес. и 4 ед. + 2 дес. и 5 ед. = 5 дес. 9 ед.

5 дес. — 50

50 + 9 = 59

Можно записать короче:

Рассуждаю так:

Число 34 представляю в виде суммы разрядных слагаемых: 30 и 4, число 25 тоже представляю как 20 и 5. Теперь начинаю вычислять:

Сначала складываю единицы:

4 + 5 = 9

Теперь складываю десятки:

30 + 20 = 50

Запись решения выглядит так:

34 + 25 = (30 + 20) + (4 + 5) = 50 + 9 = 59

34 + 25 = 59

Десятки складываются с десятками.

Единицы складываются с единицами.

Как решить пример 38 — 16?

Число 38 — можно представить как 3 дес. и 8 ед.

Число 16 — это 1 дес. 6 ед.

3 дес. 8 ед. — 1 дес. 6 ед. = 2 дес. 2 ед.

38 — 16 = (30 — 10) + (8 — 6) = 20 + 2 = 22

38 — 16 = 22

Можно рассуждать так:

Число 38 представим в виде суммы разрядных слагаемых 30 и 8, а число 16 представим так: 10 и 6. Удобно число 6 вычесть из числа 8, получим 2. Затем число 10 вычтем из числа 30, получим 20. Теперь 2 прибавим к числу 20. Получим 22.

38 — 16 = 22

Вывод:

Десятки вычитаются из десятков.

Единицы вычитаются из единиц.

Мы рассмотрели случаи устных вычислений с двузначными числами.

Познакомиться с письменными приема вычислений (сложением в столбик и вычитанием в столбик) можно в нашем справочнике.

Правило встречается в следующих упражнениях:

2 класс

Задание 22, Моро, Волкова, Рабочая тетрадь, 1 часть

Задание 28, Моро, Волкова, Рабочая тетрадь, 1 часть

Задание 79, Моро, Волкова, Рабочая тетрадь, 1 часть

Задание 111, Моро, Волкова, Рабочая тетрадь, 1 часть

3 класс

2019 — budu5.com, Буду отличником!

Нашли ошибку?

Связаться с нами

Эффективные методики

Объяснять состав числа 10 нужно постепенно, разделив обучение на несколько логичных блоков

На первых занятиях следует уделить внимание цифрам 2 и 3, их взаимоотношениям и возможным комбинациям. Далее можно переходить к занятиям с наглядными карточками и уже после подключать числовые домики

Занятие 1: осваиваем цифры 3, 2, 1

Возьмите любимые игрушки и вещи малыша (кубики, куклы, машинки). Начните упражнение с разбора числа 2 и покажите ребенку, какими способами его можно получить:

• Положите на стол перед малышом один предмет и попросите ребенка сделать так, чтобы их стало два. Обычно ему не сложно догадаться, как справиться с заданием. Если потребуется, дайте подсказку.
• Объясните малышу, что 2 является числом, состоящим всегда из пары единиц.
• Попросите ребенка выложить на стол по 2 понравившихся предмета.
• Когда двойка будет закреплена, переходите к изучению тройки. Расскажите ребенку, что если к 2 добавить 1 – получится 3. Положите перед ним две монетки и рядом еще одну. Малыш должен усвоить, что нет никакой разницы между 3 монетами вместе, 2 с 1 или 1 с 2.

Постепенно усложняйте задание. Четверку получить в игровой форме так же просто, как и тройку. Здесь могут помочь шахматы или шашки. Предложите ребенку выбрать 2 фигуры одного цвета (белый), а затем повторить задание. Спросите: сколько шахмат останется, если 1 светлую заменить на 1 темную? А что будет, если объединить 2 черные и 2 белые фигуры? В конце он должен понять, что получить число 4 можно при каждом возможном варианте перестановки.

Переходить к следующему блоку заданий стоит тогда, когда малыш поймет, что все эти действия приведут к результату известному заранее:

• 2 — это 1 + 1, 2 + 0;
• 3 — это 2 + 1, 1 + 2, 3 + 0;
• 4 — это 1 + 3, 2 + 2, 3 + 1, 4 + 0.

По такому же принципу объясните оставшиеся числа до 10.

Задание 2: числовые карточки

На этом этапе ребенок уже должен уяснить, что складывая разные цифры, можно получить любой результат. Но когда следует узнать состав определенного числа, нужно идти от обратного – от заранее выясненного ответа. Вам необходимо вместе с ним разобрать все пары слагаемых, приводящих к единому результату. Для этого отлично подойдут числовые карточки. Вариантов обучения несколько:

• Нарисуйте на карточках, например, 5 бабочек и предложите ребенку собрать нужное количество из предложенных заготовок.
• Предложите ему несколько раз самостоятельно собрать комбинации, при которых их сумма в итоге будет равняться 5.
• Попросите ребенка объяснить вам, как получить какое-либо число. Допускайте ошибки, малышам придется задействовать все свои способности чтобы их вычислить.

Приступать к последнему блоку заданий следует тогда, когда чадо сможет подбирать все варианты состава указанного числа.

Задание 3: числовые домики

Арифметические домики отлично помогают окончательно понять и закрепить в знаниях ребенка понятие о составе любого числа, а также развить навык устного счета.

Дом для чисел представляет собой здание, имеющее крышу и несколько этажей с квартирами в два ряда. Высота сооружения зависит от числа, к которому нужно подобрать все возможные комбинации цифр. Чтобы объяснить ребенку состав числа 2, достаточно нарисовать дом с двумя этажами (0+2, 1+1) и так далее.

Заготовки домиков можно найти в учебниках по математике или же изготовить самостоятельно из картона.

Как построить ход занятия:

• Положите на стол пустой дом, разместив в его крыше карточку с числом от 2 до 10 (пусть будет 6).
• Объясните ребенку, что на каждом уровне в квартирах находится столько людей, сколько написано на крыше.
• Поставьте условие: на первом этаже в 1 квартире живет всего один человек. Малышу нужно подумать и определить, сколько жильцов живет в квартире номер 2 (правильный ответ – 5).
• Теперь, когда алгоритм решения задачи ясен, попросите ребенка заселить все оставшиеся квартиры, меняя начальное количество жильцов на каждом новом этаже. В итоге на 2-м этаже будет 2 и 4 жильца, на 3-м – 3 и 3, на 4-м – 0 и 6. Таким образом, малыш сможет освоить все существующие комбинации цифр.

Небольшой лайфхак: расскажите, что любое число всегда состоит из 1 и предыдущей цифры по порядку. Так, если требуется выяснить состав числа 7, сразу готов первый ответ: 7 – это 1 и 6.

Когда все пары цифр и состав 10 будут освоены, можно усложнять задания.

Осваиваем цифры

Тему изучения цифр условно можно разделить на две составляющие: запоминание последовательности (1, 2, 3, ……. 9, 10) и графического (визуального) образа.

Как правило, последовательность цифр дети запоминают намного быстрее. Когда взрослый часто проговаривает ее, одновременно указывая по очереди на какие-нибудь предметы, ребенок быстро запоминает на слух названия чисел и их порядок, начинает повторять те же действия и таким образом учится считать. Однако есть множество упражнений, чтобы этот процесс ускорить и закрепить навык. Вот некоторые из них:

1. Считать все, что попадается на глаза Нужно предлагать ребенку считать все, что его окружает в течение дня: ступеньки в подъезде, голубей во дворе, карандаши в пенале, машины на стоянке, пуговицы на одежде, людей в очереди к кассе и так далее. Чем чаще ребенок это делает, тем быстрее информация уложится в его памяти, а также появится понимание взаимосвязи между цифрой (ее названием) и конкретным количеством.

2. Пальчиковые игры В изучении цифр от 1 до 10 самым лучшим инструментом являются пальчики. Кроме того, что их можно просто посчитать, разгибая по очереди, есть еще большое количество пальчиковых игр, направленных как на тренировку навыка устного счета, так и на развитие мелкой моторики и воображения.

3. Стишки, песенки, считалочки Запоминание последовательности чисел с помощью песен, стихов или считалочек позволяет воспринимать информацию не только на слух, но и через зрительные образы, которые рисует воображение ребенка. Это ускоряет процесс изучения и хорошо развивает фантазию.

Если во время изучения чисел у ребенка возникают трудности, чаще всего они связаны с визуальным запоминанием. Особенно это касается внешне похожих друг на друга цифр, таких как 6 и 9, 1 и 7. Чтобы быстро запомнить графический образ цифры, также есть много разных секретов:

4. Ассоциации Простой и эффективный способ, чтобы запомнить внешний вид цифры – найти сходство с каким-либо объектом, придумать ассоциацию. К примеру, цифра 8 похожа на матрешку, бантик, снеговика или медвежонка. Цифра 2 напоминает лебедя, 4 – перевернутый стул или клюв. Здесь нет предела фантазии, у каждого ассоциации будут свои.

5. Распознать на ощупь Цифры должны быть объемные. Можно сделать их самостоятельно из подручных материалов или приобрести уже готовые. Их нужно сложить в мешочек или коробочку, из которой ребенок будет доставать по одной не глядя и пытаться на ощупь определить, что за цифра ему попалась.

6. Рисунок на спине Для игры нужны двое. Взрослый на спине ребенка рисует пальцем какую-нибудь цифру, а тот должен ее отгадать. Затем можно поменяться местами.

7. Игрушечные цифры Они могут быть магнитными, мягкими, нарисованными на кубиках – в зависимости от того, что больше нравится. Из них можно выстраивать последовательность от 1 до 10, называя вслух каждую цифру, расставлять в обратном порядке или вразброс, находя ту цифру, которую называет взрослый.

8. Цифры вокруг Каждый день ребенку встречаются разные цифры: в номерах домов, автомобилей, на различных плакатах и объявлениях

Если обращать на них внимание и проговаривать, то это также будет способствовать запоминанию

После того, как ребенок научился считать и запомнил все цифры, можно переходить к изучению состава чисел.

Как организовать математическую подготовку к школе

Чтобы ребёнок, придя в первый класс, имел хороший уровень подготовки, нужно уделять время домашним занятиям. Рекомендуется запастись карточками с цифрами, кассой счёта, мелкими бусинами разных форм и т. д. *Занятия нужно проводить в игровой форме. Начинают с формирования математических представлений. После подготовительного этапа переходят к изучению цифр и счёта.# По каждым теме есть большой выбор обучающих пособий, соответствующих возрастным особенностям дошкольников. Кроме того, если ребёнок посещает детский сад, там проводится подготовка в школе. Родителям остаётся в этом случае лишь заниматься дополнительно. Или отвести ребёнка на специальные в центрах дополнительного образования. Педагоги на таких курсах знают все государственные образовательные стандарты и со знанием дела готовят дошкольников к школьному обучению.

Дошкольника нужно заинтересовать математикой в период подготовки к школе. Родители должны продемонстрировать пользу от знания счёта. *Можно брать ребёнка в магазин, позволяя самому выбрать некоторые покупки с учётом имеющейся суммы. Если счёт станет для малыша увлекательным, интересным занятием, он будет часто практиковаться в нём.# Сформированный интерес к математике – хороший старт для обучения в школе. Ребёнок с удовольствием будет учиться и открывать в себе новые способности.

Справочно:

Материалы подготовлены Федеральным образовательным сервисом «ИнПро» (Лицензия Минобрнауки 22Л01 № 0002491). Готовим детей к школе по всей России в 40+ центрах и онлайн, в том числе в г. Занятия в Вашем городе.

Бесплатная горячая линия: 8 800 250 62 49 (с 6 до 14 по Мск).

• «Вконтакте»:
• «Одноклассники»:
• «Инстаграм»:
• «YouTube»:

Как наглядно объяснить дошкольнику состав числа?

Для успешного освоение математики в школе следует постараться научить сына или дочку простейшему счету до поступления в школу. Начинать нужно с представления чисел и их графического обозначения – цифр. Последних всего десять – от 0 до 9, и число 10 состоит из цифр 1 и 0, которые обозначают количество чего-либо (конфет, кубиков, яблок).

Выучить цифровой ряд до 10 туда и обратно в ходе игры и практических действий можно за несколько вечеров

Чтобы малыш сразу усвоил, как он формируется, важно объяснить, что каждое последующее число отличается от предыдущего в сторону увеличения (при счете от 0 до 9) или уменьшения (при счете в обратном направлении). Это научит его отличать порядковые и количественные числительные (например, четвертый в числовом ряду или четыре предмета)

Закладка понятий сложения и вычитания

Закладка понятий сложения и вычитания выполняется системно, с применением специально составленных примеров, которые разрешаются с применением предметно-практичекого деяния. На основании школьных программ, все действия в арифметике определяются именно примерами, обозначающими конкретику арифметических действий – складывать, отнимать, умножать или делить.

Решение примеров значительно увеличивает культуру вычисления у ребенка. В этом процессе у него складывается умение и навыки модуляции реальных предметов и явлений, накладывания на математический лад определенных ситуаций.

В начальной школе формируется основа знаний, умений учеников, которые необходимы не только для предстоящего учения, но и для совершенствования качеств ума, морали, воли и эмоций.

Следует начинать решать примеры с определенных этапов

Для начала очень важно, чтобы ребенок твердо понял, что «сложение» обозначает объединение количеств, а «вычитание» — совсем противоположная процедура, обозначающая отделение от множества предметов определенной его части. То есть в этом случае мы забираем, зачеркиваем, закрываем

Дети должны понимать, что можно найти при сложении или отнимании, в каком случае станет больше, а в каком – меньше, какими знаками в математике определяются эти действия

При этом можно использовать линейку, отнимая или складывая, двигаться по ней в соответствующую сторону

Дети должны понимать, что можно найти при сложении или отнимании, в каком случае станет больше, а в каком – меньше, какими знаками в математике определяются эти действия. При этом можно использовать линейку, отнимая или складывая, двигаться по ней в соответствующую сторону.

Дальше рекомендуется проводить работу над определениями предметов, их количества и соответствующих цифр. Обучающиеся должны осознавать разницу среди количества предметов и цифрами, которыми они обозначаются.

Правильно организованная работа над выражением создаст основу для восприятия условия примера (задачи).

В этом случае можно воспользоваться определенными выражениями – составлять выражение по рисунку с необходимыми пояснениями, стрелками обозначая перемещение их внутрь контура или из него (прибавить или отнять). Со временем слова и рисунки заменяем цифрами и знаками и пробуем по ним составить короткий рассказик, чтобы ребенок мог правильно понять, что необходимо сделать.

Можно применить методику примеров в стихотворной форме. Дети должны слушать и фишками откладывать все прозвучавшие цифры. После этого логическими рассуждениями производится необходимое действие и получается искомый результат.

Наибольшего эффекта можно достигнуть, если обучать решению примеров вы станете в форме словесных задачек, при этом использовать компьютерные технологии. Такие примеры можно применять несколько раз, легко меняя условия, создавая удобство для устных вычислений. Это помогает и самим ученикам, которым трудно раньше было проводить необходимые вычисления в уме. Решение примеров приучает к вниманию и умению анализировать, определять главные элементы.

Одним словом, примеры должны быть увлекательными и вполне доступными для учеников, но одновременно не совсем легкими, заставляющими думать и анализировать.
При получении положительных результатов в решении примеров, можно переходить к более усложненным заданиям.

Определение понятия «состав числа»

Состав числа — это разбиение числа на его составляющие части: последовательность цифр, из которых оно состоит.

1. Цифры числа вместе образуют его состав.
2. Символы и цифры числа можно считать его составом.

Рассмотрим примеры чисел и их состава:

Число	Состав
125	1, 2, 5
9876	9, 8, 7, 6
42	4, 2

Чтобы правильно определить состав числа, нужно учитывать порядок следования цифр. Например, состав числа 327 будет следующим:

1. 3 (единицы)
2. 2 (десятки)
3. 7 (сотни)

Понимание состава числа и его разбиение на составляющие цифры помогает детям изучать системы счисления, основные операции арифметики и другие математические понятия.

Примеры разложения числа на составляющие

Пример 1:

• Число: 12
• Составляющие: 10 и 2

Пример 2:

• Число: 54
• Составляющие: 50 и 4

Пример 3:

• Число: 87
• Составляющие: 80 и 7

Пример 4:

• Число: 33
• Составляющие: 30 и 3

Пример 5:

• Число: 75
• Составляющие: 70 и 5

Для разложения числа на составляющие обычно используются десятки и единицы. Один из способов разложения — разложение на десятки и единицы. Например, для числа 24 — это десятки (20) и единицы (4). Это помогает детям понять, что число 24 состоит из 20 и 4.

Также можно использовать другие разложения, например, на сотни, десятки и единицы. Но на первых порах обычно ограничиваются разложением на десятки и единицы.

Разложение чисел на составляющие является важным навыком для детей первого класса, так как это помогает им лучше понимать структуру чисел и учиться выполнять математические операции, такие как сложение и вычитание.

Как понять состав числа?

Состав числа – это разложение числа на числовые составляющие, такие как цифры и разряды. Понимание состава числа является важным навыком для учеников первого класса, так как это помогает им понять структуру числовых значений и развивает базовые навыки математического анализа.

Процесс понимания состава числа может быть представлен с помощью следующих шагов:

Рассмотрите число и определите, из каких цифр оно состоит
Например, число 523 состоит из трех цифр: 5, 2 и 3.
Обратите внимание на значения каждой цифры по отдельности

Например, цифра 5 в числе 523 имеет стоимость 500, цифра 2 имеет стоимость 20, а цифра 3 имеет стоимость 3.
Понимание разрядов числа также является важной частью его состава
Например, в числе 523 разряды это сотни, десятки и единицы.
Определите значение каждого разряда числа. Например, в числе 523 цифра 5 находится в разряде сотен, цифра 2 находится в разряде десятков, а цифра 3 находится в разряде единиц.

Понимание состава числа помогает ученикам не только овладеть базовыми математическими навыками, но и использовать эти знания для решения сложных математических задач. Например, зная состав числа, ученик может разложить его на сумму разрядных значений и выполнить операции сложения или вычитания.

Число	Разряды	Значения разрядов
523	Сотни, десятки, единицы	500, 20, 3
415	Сотни, десятки, единицы	400, 10, 5

Использование различных математических игр и упражнений, таких как сортировка цифр, решение головоломок или задач на состав чисел, помогает ученикам развивать навыки понимания состава чисел и делает процесс обучения более интересным и вовлекающим.

Зачем нужно знать состав числа?

Знание состава числа является важным элементом в изучении математики для учащихся первого класса. Этот навык помогает детям развить понимание чисел, их свойств и отношений, а также способствует развитию логического мышления.

Состав числа описывает его способ записи через сложение или вычитание других чисел. Например, число 9 может быть представлено как сумма 5 и 4, или 6 и 3. Зная состав числа, ребенок сможет легко выполнять арифметические операции, такие как сложение и вычитание.

Знание состава числа также позволяет детям лучше понять математические отношения и свойства чисел. Например, ребенок может увидеть, что число 6 состоит из двух равных частей — 3 + 3, или из трех равных частей — 2 + 2 + 2. Это поможет ему понять понятия четности и нечетности чисел, а также сделать первые шаги в изучении умножения и деления.

Знание состава числа помогает развить логическое мышление у детей. Например, ребенок может решить задачу, используя разные комбинации чисел для достижения нужного результата. Он также сможет легче анализировать и решать математические задачи, так как будет понимать, как число может быть представлено через другие числа.

В целом, знание состава числа является фундаментальным навыком в изучении математики и помогает детям развивать не только математические, но и логические навыки.

Дидактический материал для ознакомления с составом числа из единиц в старшей группе

Нелля Ткаченко

Дидактический материал для ознакомления с составом числа из единиц в старшей группе

Дидактический материал для ознакомления

с составом числа из единиц в старшей группе.

ЦЕЛЬ:

Формирование представлений о составе числа в пределах первого пятка.

ЗАДАЧИ:

— закрепить,-

— представления о числах и цифрах в пределах первого пятка;

— развивать,-

— представления, что все числа составляются из единиц;

— представления, что количество единиц в разных числах различно;

— внимание, зрительное восприятие, память, логическое мышление;

— мелкую моторику;

— воспитывать,-

— организованность;

— сосредоточенность;

— интерес к математическим играм;

Счетная деятельность у детей пятилетнего возраста в процессе систематического обучения уже объективно совершенна. Изучение состава числа из единиц в старшей группе – это подготовка к освоению вычислительного приема – присчитыванию и отсчитыванию по единице.

Изучение состава чисел из единиц необходимо начинать от анализа состава множества из элементов к составу числа из единиц, при этом надо быть последовательным, не торопиться, именно с пятка – с каждого числа –от 2 до 5 (2,3,4,5)

. В качестве наглядногоматериала подбирается группа одного вида предметов, в которой каждый отличается друг от друга качественными признаками (например, цветом, размером) . Так же, в последующем, используются предметы,объединенные одним понятием, например, игрушечные комплекты одежды, посуды, мебели и т. п. Наряду с сюжетными предметами можно использовать модели геометрических фигур, полоски бумаги разной длины и величины и т. д. Необходимо научить детей, рассматривая множества, рассказывать, как эта группа составлена, называть каждый элемент и их общее количество.

Например:

«Число 4 составлено так: 1 зеленый кружок, 1 красный кружок. 1 желтый кружок, 1 синий кружок – всего 4 кружочка».

Пересчитав 4 кружочка, ребенок должен рассказать, как составлено «это четыре»

, подчеркивая количественныйсостав: один – зеленый, один – красный, один – желтый, один – синий, всего – четыре. Предлагая детям выполнять задания с различными видами групп предметов, надо просить рассказывать, как составлена группа, сколько в ней разных предметов и сколько их всего, называть и предметы и их количество. Постепенно от более конкретных вопросов надо переходить к общим – «Сколько ты взял? Сколько … всего? Как у тебя получилось… (например, 5, карандашей?»

Изучая количественный состав числа из единиц, надо обратить внимание детей, что единица может отражать не только отдельный предмет, а может быть отражением целой группы предметов. Например, предложить детям рассмотреть множество геометрических фигур и ответить на вопросы,-

— Из каких частей составлено это множество? («Составлено из трех частей»

— Из каких частей составлено это множество? («Составлено из трех частей»

— Назовите цвет и количество частей данного множества. («В данном множестве три части разного цвета: одна часть – треугольники красного цвета, одна – треугольники синего цвета, одна – треугольники зеленого цвета. Всего три части».

— Из скольких единиц состоит число три? («Из трех отдельных единиц»

).

В данном задании дети должны осознать, что единица может отражать не только один отдельный предмет, но и одну группу предметов.

В процессе ознакомления детей с составом числа из единиц, можно использовать словесные упражнения,-

— на полянке собрались лесные животные: один заяц, один ежик, одна белочка. Сколько всего собралось животных на полянке в лесу? По сколько разных лесных животных собралось на полянке и т. д.

И другие задания, например,-

— подберите пять треугольников разного цвета;

— нарисуйте три разные геометрические фигуры;

— поставьте на стол четыре разные куклы и тд.

Ознакомление детей с составом числа идет в последовательной системе занятий, что создает условия для образования новых связей, формирующих знания детей о количественном составе, что в свою очередь является подготовкой к вычислительной деятельности.

Как объяснить ребенку состав числа?

Современная программа обучения в школе задает для будущих первоклассников достаточно высокую планку. Придя в школу, ребенок уже должен иметь определенный багаж знаний и навыков, одним из которых является понимание состава числа.

Состав числа – это возможность раскладывать числа от 1 до 10 на два меньших числа. Этот навык заложит фундамент, благодаря которому ребенку в будущем будет легче осваивать математику, например, сложение и вычитание. Если уделять время занятиям и постепенно осваивать эту тему, то результат не заставит себя ждать. А математические тренажеры помогут в усвоении новых знаний.

Чтобы ребенок мог успешно освоить эту тему, он уже должен узнавать графические образы цифр, уметь считать от 1 до 10 и, желательно, от 10 до 1 в обратном порядке. Также плюсом будет возможность самостоятельной записи ребенком цифр.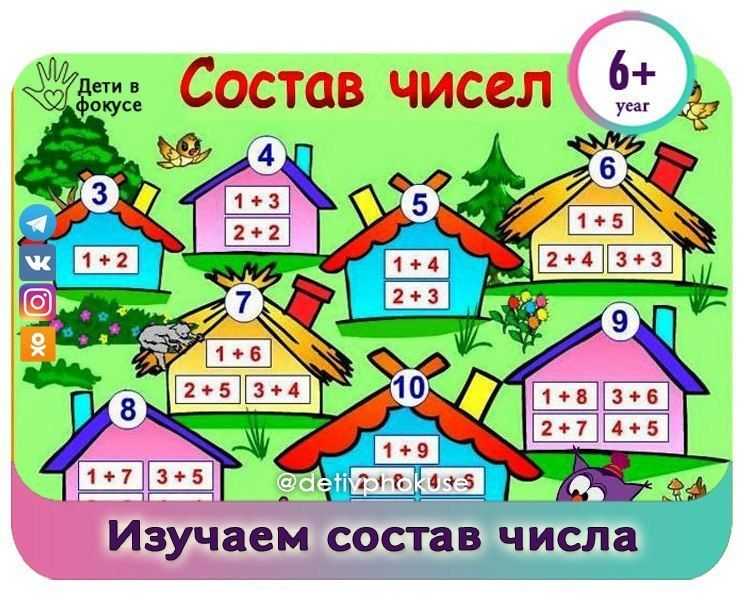

Состав числа в пределах 10

Засели домик цифрами

Состав числа в пределах 20

Для чтобы осваивать состав числа ребенку было интересно и увлекательно, можно воспользоваться проверенными методами и упражнениями.  Например, числовые карточки. На них изображено число и предметы, количество которых ему соответствует. Они наглядно иллюстрируют состав чисел, поэтому рекомендуем начать знакомство с темой с них.

Объяснять ребенку основы сложения можно помощью подручных предметов – пуговиц, камушков, конфет и т.д. Пригодятся здесь и числовые карточки: например, на одной из них изображено 1 яблоко, а на другой – 2 апельсина. Если сложить их вместе, то сколько фруктов получится? Ребенок посчитает все фрукты и назовет сумму, постепенно запоминая результаты сложения разных чисел.

Когда ребенок начнет понимать, как складывать предметы, можно перейти к разбору состава числа. Родитель говорит, сколько предметов должно получиться в итоге, начиная с маленьких чисел,  а потом помогает ребенку собрать необходимое количество. Например, нужно собрать 4 банана. Берем карточку с изображением одного банана и спрашиваем, сколько еще нужно собрать. Затем добавляем карточку с двумя бананами и повторяем вопрос. Так вместе с ребенком вы переберете разные комбинации и освоите базовые составы числа.

Постепенно переходите к большим числам, где вариативность комбинаций увеличивается. Многократное проведение такого упражнения поможет закрепить в памяти состав числа и ребенок сможет легко его воспроизводить. Потом можно поупражняться таким же методом в вычитании. Взять несколько карточек например, 1 яблоко, 3 яблока и 4 яблока. Спросить у ребенка, сколько яблок на всех этих карточках. И спросить, какую карточку нужно убрать, чтобы получилось 7  яблок.

Для закрепления темы хорошо подойдут числовые домики – это следующий этап освоения состава чисел. Домик, где живут цифры, имеет несколько этажей с двумя окошками на каждом. На крыше находится число, которое разбивается на два числа-соседа на каждом этаже. Количество этажей зависит от количества возможных комбинаций, на которые можно разложить требуемое число.

Можно нарисовать такой домик самостоятельно. Например, для числа 4 будет 2 этажа: на одном числа-соседи – 2 и 2, на втором – 1 и 3. А можно воспользоваться готовыми числовыми домиками, где ребенку нужно будет только найти подходящие цифры соседи.

Начинать можно с первого или последнего этажа. Если у ребенка поначалу задание вызовет трудности, можно помочь ему, заполнив некоторые этажи. Позже можно объяснить секрет домика: переходя на этаж число становится на 1 больше или меньше.

После усвоения состава чисел до 10, можно переходить ко второму десятку, если ребенок уже его знает.

При занятиях с ребенком важно помнить, что успех складывается из регулярности и поддержки. Хвалите его за успешные решения, это отлично мотивирует! Поддерживайте в трудных моментах и относитесь с пониманием к ошибкам

Так, небольшими шажочками и с вашей поддержкой, тема «Состав числа» будет успешно освоена ребенком.

Композиция функций

«Композиция функций» — это применение одной функции к результатам другой:

Результат f() передается через g()

Записывается: (g º f)(x)

Что означает: g(f(x))

Пример:

f(x) = 2x+3 g(x) = x 2

“x” просто заполнитель . Чтобы избежать путаницы, давайте просто назовем это «ввод»:

f(ввод) = 2(ввод)+3

g(ввод) = (ввод) 2

Начнем:

Сначала мы применяем f, затем применяем g к этому результату:

(g º f)(x) = (2x+3) 2

Что, если мы обратный порядок f и g?

(f º g)(x) = f(g(x))

Сначала мы применяем g, затем применяем f к этому результату:

(f º g)(x) = 2x 2 + 3

Получаем другой результат!

Когда мы меняем порядок, результат редко бывает таким же.

Будьте осторожны, какая функция стоит первой.

Символ

Символ композиции — маленький кружок:

(g º f)(x)

Это , а не закрашенная точка: (g · f)(x), так как это означает, что умножается на .

Составлено с самим собой

Мы можем даже составить функцию с самим собой!

Пример:

f(x) = 2x+3

(f º f)(x) = f(f(x))

Сначала мы применяем f, затем применяем f к этому результату:

(f º f)(x) = 2(2x+3)+3 = 4x + 9

Мы должны сделать это без красивой диаграммы:

(f º f)(x)= f( е (х))

 = f(2x+3)

 = 2(2x+3)+3

 = 4x + 9

Доменов

До сих пор это было легко, но теперь мы должны рассмотреть Доменов функций .

Домен — это набор всех значений , которые входят в функцию.

Функция должна работать для всех значений, которые мы ей даем, поэтому зависит от нас, , чтобы убедиться, что мы правильно определили домен!

Пример: домен для √x (квадратный корень из x)

Мы не можем получить квадратный корень из отрицательного числа (если только мы не используем мнимые числа, а это не так), поэтому мы должны исключить отрицательных чисел:

Домен √x неотрицательный Действительный Числа

На числовой строке это выглядит так:

Используя нотацию конструктора множеств, записывается:

{ x | x ≥ 0}

Или, используя интервальную запись, это:

[0,+∞)

Важно правильно указать Домен, иначе мы получим плохие результаты!

Домен составной функции

Мы должны получить оба домена правильно (композитная функция и первая используемая функция).

При выполнении, например, (g º f)(x) = g(f(x)):

• Убедитесь, что мы правильно получили домен для f(x) ,
• Затем также убедитесь, что g(x) получает правильный домен

Пример:

f(x) = √x g(x) = x 2

Домен f(x) = √x — все неотрицательные действительные числа

Домен g(x) = x 2 — все действительные числа

Составная функция:

(g º f)(x) = g(f(x))

 = (√x) 2

 = x

Теперь “x” обычно имеет домен всех действительных чисел …

… но поскольку это составная функция , мы должны также учитывать f(x) ,

Таким образом, домен состоит из неотрицательных действительных чисел

Почему оба домена?

Ну представь функции машины… первая проплавляет отверстие пламенем (только для металла), вторая просверливает отверстие побольше (работает по дереву или металлу):

То, что мы видим в конце, это просверленное отверстие, и мы можем подумать, что “это должно подойти для дерева или металла “. Но если мы подложим дрова в g º f, то первая функция f разожжет огонь и все сожжет!

Так что то, что происходит “внутри машины”, очень важно

Функция декомпозиции

Мы можем пойти другим путем и разбить функцию на композицию других функций.

Пример:

(x+1/x) 2

Эту функцию можно составить из следующих двух функций:

f(x) = x + 1/x

g(x) = x 2

И получаем:

(g º f)(x) = g(f(x))

 = g(x + 1/x)

 = (x + 1/x) 2

Это может быть полезно, если исходная функция слишком сложна для работы.

«Композиция функций» — это применение одной функции к результатам другой.
(g º f)(x) = g(f(x)) , сначала применить f(), затем применить g()
Мы также должны учитывать домен первой функции
Некоторые функции можно разложить на две (или более) более простые функции.