Роль музыки в воспитании ребенка
Даже простое прослушивание музыки активизирует участки мозга, связанные с сочувствием и позитивным мышлением. Нейронаучные исследования показали, что при этом высвобождается гормон дофамин — нейротрансмиттер, который активирует центр удовольствия в мозгу.
Совместная “музыкальная деятельность” создает доверие между ее участниками и делает их ближе. Эта синхронизация выходит за рамки повседневного опыта.
Есть много способов, которыми родители и дети могут общаться посредством музыки. Вот несколько из них:
Пение
Пение в отношениях родителей и детей начинается с колыбельных. Родителям рекомендуется как можно чаще петь их своим маленьким детям.
Пение малышам не только развивает связь с ними, оно также жизненно важно для развития языковых способностей детей. С детьми постарше можно уже петь вместе
Совместное пение увеличивает синхронизацию друг с другом. Это отличное занятие для поездок, посиделок у костра и семейных вечеров
С детьми постарше можно уже петь вместе. Совместное пение увеличивает синхронизацию друг с другом. Это отличное занятие для поездок, посиделок у костра и семейных вечеров.

Вот несколько песен, которые вы и ваши дети могли бы спеть прямо сейчас:
Песенка бременских музыкантов
Голубой вагон бежит-качается
Просыпается заря
Я верю
Танцы
Танцы с детьми начинаются с того, что вы поднимаете малыша, поете и кружите его по комнате.
Ищите песни, которые нравятся вашим детям, пойте и танцуйте под них вместе. Пусть дети школьного возраста научат вас танцевать под песни, которые нравятся им. И, конечно, не забывайте о старых произведениях — хитах всех возрастов.
Танцы — это отличная замена прожиганию времени у телевизора.
Совместное прослушивание музыки
Слушать музыку вместе очень полезно. Познакомьте своих детей с прослушиванием классической музыки. На YouTube есть несколько фантастических видеороликов, которые знакомят детей всех возрастов с классикой.
Походы на концерты
Ходить на концерт вместе — это прекрасный способ по-особому провести время со своими детьми. Если в вашем городе проходят выступления симфонического оркестра, сходите туда с детьми.
Многие оркестры предлагают специальные программы для детей, чтобы познакомить их с классикой. Эти программы забавны и, как правило, предназначены для сближения детей и родителей.

Также ищите концерты и других видов музыки (например, рок или кантри) для посещения со старшими детьми. Музыкой можно влиять на воспитание детей всех возрастов!
Игра на музыкальных инструментах
Участие родителей в обучении служит стимулом для детей. И, как мы уже писали ранее, обучение музыке способствует улучшению когнитивных функций и развитию социальных навыков, причем это касается как детей, так и их родителей!
Будет прекрасно, если музыка станет вашим общим хобби.
Практическое применение
Изучение взаимосвязи между музыкальными структурами и математическими концепциями имеет практическое применение в различных областях.
В образовании и исследованиях математика и музыка могут быть интегрированы для поддержки развития критического мышления и умения решать проблемы. Изучение математических концепций через музыку может сделать обучение математике более интересным и доступным.
В музыкальной терапии математические аспекты музыки могут использоваться для лечения различных неврологических и психологических состояний. Музыкальные структуры и ритмы могут помочь в стабилизации настроения, снижении уровня стресса и повышении концентрации.
В композиции и создании музыки математические принципы могут быть использованы для создания уникальных звуковых ландшафтов и хармонических структур. Композиторы могут экспериментировать с математическими моделями, пропорциями и алгоритмами для создания новых и инновационных музыкальных произведений.
В индустрии звукозаписи и звукотехнике математические методы используются для обработки и улучшения качества звука. Цифровая обработка звука с помощью математических алгоритмов позволяет устранять шумы, обеспечивать балансировку звуковых компонентов и создавать эффекты.
Таким образом, изучение взаимосвязи между музыкальными структурами и математическими концепциями имеет широкий спектр практического применения, от образования и терапии до композиции и звукоинженерии.
Музыкальное образование и математическое развитие
Музыкальное образование имеет сильную связь с математическим развитием учащихся и может способствовать их успехам в области математики.
Изучение музыки подразумевает работу с такими математическими концепциями, как ритм, длительность, темп, метрика и гармония. Ритмические фигуры и музыкальные фразы подчиняются определенным математическим закономерностям и представляют собой последовательности временных интервалов, которые можно измерять и анализировать.
Изучение нот и музыкальных символов требует умения читать знаки и символы, делать численные вычисления и применять математические пропорции. Ученикам приходится анализировать музыкальные фрагменты, распознавать структуры и создавать логические связи между ними.
Кроме того, музыкальное образование развивает учеников в области пространственного мышления, координации движений и решения проблем. Игра на инструменте или исполнение музыкальной композиции требует точности и синхронизации движений, что требует работы с числами и математическими понятиями.
Таким образом, музыкальное образование может эффективно способствовать развитию математических навыков и концепций учащихся. Оно помогает ученикам лучше воспринимать и понимать математические абстракции, развивает их аналитическое мышление и способность к решению задач.
Использование музыки в математических задачах
Музыка может быть использована в математических задачах для усиления понимания и применения различных математических концепций.
Один из способов использования музыки в математике — это изучение и применение ритма. Ритм может помочь студентам лучше понять и сравнивать длительности и соотношения между числами, также как и математические пропорции и сравнения.
Другой подход — это работа с музыкальными фразами и мелодиями для развития навыков работы с последовательностями и шаблонами, что может иметь отношение к алгебре и паттернам.
Также музыка может быть использована в геометрии и физике. Например, звук распространяется в пространстве в волновых формах, а изучение звуковых волн может помочь студентам лучше понять геометрические концепции, такие как периоды, амплитуды и длины волн.
Использование музыки в математических задачах может сделать учебный процесс более интересным и занимательным, способствуя более глубокому пониманию математических концепций и улучшению решения проблем.
Немножко истории
Вы не поверите, но эта система просуществовала на протяжении 12 веков! Дольше, чем любая другая известная музыкальная система. Вот только музыкантов постоянно бесила так называемая волчья квинта. Дело в том, что если в системе Пифагора отложить квинту 12 раз, то мы должны получить исходную ноту, просто на 7 октав выше. Но на самом деле мы получим чуууть-чуть более высокую ноту, ведь $\left(\frac{3}{2}\right)^{12} \approx 129.746$, что чуть больше, чем $2^7=128$. Накопленную разницу называли пифагорейской коммой, и чтобы избавиться от неё, частоту какой-нибудь одной ноты немного подкручивали. В итоге одна из квинт внутри октавы получалась короче остальных и звучала абсолютно отвратительно, будто волки воют…
В итоге музыканты тех времён просто старались не играть смещённую ноту :-). Из-за этого было сложнее менять тональности у произведений, сложнее настраивать инструменты и тяжелее импровизировать. Неудивительно, что рано или поздно кто-то должен был придумать что-то ещё.
Этим кем-то стал Андреас Веркмейстер. Он сформулировал задачу так. Первое: нужно сохранить в октаве двенадцать традиционно устоявшихся звуков. Всё-таки 12 веков музыкальной истории так просто на помойку не выкинешь. Второе: никакой коммы быть не должно. И третье: все соотношения между соседними частотами должны быть абсолютно равными. Вот это было поистине революционное решение!
Математически Веркмейстер взял октаву с соотношением 1 к 2 и распределил её поровну между 12 нотами. Если две соседние ноты отличаются по своей частоте в $x$ раз, то $x^{12} = 2$, а значит, $x = \sqrt{2}$, вот и всё.
Частота ноты до-диез — это частота до, умноженная на $\sqrt{2}$. Частота ноты ре, следующей после до-диеза, это частота до-диеза, умноженная ещё на $\sqrt{2}$. И так далее! Через 12 нот получается идеальная октава.
Такие образом, Веркмейстер по сути равномерно распределил Пифагорову комму между всеми звуками внутри каждой октавы. Комма рассосалась и стала незаметной. Но досталось это счастье большой ценой: внутри октавы не осталось ни одного чистого интервала. Даже квинта — интервал, тысячелетиями считавшийся незыблемым — стала чуть короче, теперь она равна не $\frac{2}{3}$, а $\frac{1}{\sqrt{2}^7}$, то есть примерно $0,66742$.
Многих музыкантов поначалу возмутило предложение Веркмейстера. Однако через 30 лет почти все смирились с компромиссом, потому что разница между чистой настройкой и той, что предложил Веркмейстер, была едва уловимой, а достоинства нового строя постепенно стали очевидными. Исчезла волчья квинта. Стало возможным переходить из тональности в тональность и из мажора в минор как угодно. В ладу (например, в до-мажоре) остались те же семь основных звуков, но теперь лад мог начинаться с любой клавиши, хоть с белой, хоть с черной. Впервые делом доказал это великий Бах, написав цикл произведений для всех двадцати четырех тональностей — двенадцати минорных и двенадцати мажорных. До реформы Веркмейстера такое количество тональностей существовало лишь теоретически, а на практике было невыполнимо, ибо пришлось бы чуть не для каждой из них заново перестраивать инструмент.
Немножко математики
Окей, с октавами разобрались. Но откуда берутся остальные ноты внутри октавы? На самом деле они появляются достаточно естественным образом. Мы только что выяснили, что обертоны для ля первой октавы звучат на частотах 880 Гц, 1320 Гц и 1760 Гц. Про 880 Гц и 1760 Гц нам уже всё понятно — это ля второй и третьей октавы. А вот что такое 1320 Гц? Если частоты нот ля второй и третьей октавы относятся друг к другу как 1 к 2, то частота этой лежащей между ними ноты соотносится с ними как 2 к 3 и 3 к 4 (а $\frac{2}{3} \times \frac{3}{4}$ как раз равно $\frac{1}{2}$ — радует, что математически мы ещё нигде не ошиблись). Эта промежуточная нота — нота ми. На самом деле это не совсем современная нота ми, но мы об этом поговорим позже. Пока давайте считать, что это честная ми, образующая квинту с ля второй октавы и кварту с ля третьей октавы. Названия «квинта» и «кварта» на самом деле появятся позже, но уже сейчас нам нужно как-то обозначать музыкальные интервалы (промежутки между двумя нотами), вот давайте и воспользуемся правильными названиями: интервал между нотами с соотношением основных частот 2 к 3 будем называть квинтой, а с соотношением 3 к 4 — квартой.
Получается, что обертоны располагаются следующим образом: первый — через октаву после базового тона, второй — через квинту после первого обертона и третий — через кварту после второго (что то же самое, что через две октавы после базового тона). Ну а дальше аналогично появляются и остальные интервалы — большая терция (интервал с соотношением частот 4 к 5) и малая терция (5 к 6). Чтобы можно было сыграть такие интервалы на наших инструментах, внутри октавы появляются и другие ноты.
Вот только незадача — у музыкантов и математиков никак не получалось выбрать конечное (и желательно небольшое, конечно) количество нот и расположить их внутри октавы так, чтобы любая пара нот давала один из приятных интервалов, описанных выше, или составлялся из нескольких таких. То там, то сям что-нибудь не клеилось.
Одной из первых успешных попыток решить эту задачу считают Пифагоров строй. Пифагор расположил семь нот внутри октавы со следующими соотношениями частот между парами соседних нот:
$$
\frac{8}{9} \hspace{4em} \frac{8}{9} \hspace{4em} \frac{243}{256} \hspace{4em} \frac{8}{9} \hspace{4em} \frac{8}{9} \hspace{4em} \frac{8}{9} \hspace{4em} \frac{243}{256}
$$
Понятно, кстати, откуда здесь взялась дробь $\frac{8}{9}$ — это разность между двумя главными (после октавы, конечно) интервалами: квинтой и квартой.
$$\frac{2}{3} : \frac{3}{4} = \frac{8}{9}$$
В Пифагоровом строе не всё гладко — во-первых, эти двести-сорок-три двести-пятьдесят-шестых, которые появились как число, которого не хватало в ряду, чтобы произведение чисел во всём ряду было равно $\frac{1}{2}$. Смотрите: $\left(\frac{243}{256}\right)^2 \times \left(\frac{8}{9}\right)^5 = \frac{3^{5 \times 2}}{2^{8 \times 2}} \times \frac{2^{3 \times 5}}{3 ^ {2 \times 5}} = \frac{1}{2}$.
Во-вторых, фишкой пифагоровского строя было то, что от любой ноты можно было отложить не только октаву, но и чистую квинту, ведь $\frac{8}{9} \times \frac{8}{9} \times \frac{243}{256} \times \frac{8}{9} = \frac{1}{2}$. Исключение составляла только нота си, от неё квинта не откладывалась.
Пифагор попытался решить эту проблему добавлением в строй ещё пяти нот, тем самым разбив каждый из интервалов, равных $\frac{8}{9}$, на два более мелких интервала. С математической точки зрения он построил замыкание множества частот относительно операции откладывания квинты (то есть умножения и деления на $\frac{2}{3}$). Квинта от ля — это ми, квинта от ми — это си, но уже следующей октавы. Чтобы «вернуть» си в нашу октавы, просто делим частоту на два и продолжаем.
Влияние музыки на развитие мозга
Обучение музыке в раннем возрасте (до семи лет) вызывает реальные физические изменения в структуре и функциях мозга. Известно, что при этом увеличивается белое вещество в мозолистом теле, что приводит к увеличению связности мозга.
Также раннее музыкальное обучение способствует увеличению серого вещества в коре головного мозга, особенно в сенсорно-моторной области.
Музыка и воспитание детей
Музыка улучшает эмоциональную регуляцию и способность быстро реагировать на события. Это повышает способность ребенка справляться с разочарованиями и избегать чрезмерных стрессов.
Одним из последних открытий нейровизуализации является то, что даже краткая музыкальная тренировка приводит к увеличению кровотока в левой части мозга
Это, например, приводит к улучшению языковых способностей, когнитивных функций, включая внимание, и зрительно-пространственного восприятия

Из-за возросшего интереса к взаимосвязи между музыкой и мозгом была создана целая область исследований — нейромузыкология.
Все исследования, проведенные за последние несколько лет, сходятся в одном — музыка активирует каждую известную область мозга и способствует ее развитию.
Известно, что мозг музыкантов больше, чем у среднестатистических людей. Они обладают превосходной рабочей памятью, слуховыми навыками и когнитивной гибкостью. С течением времени музыка «перестраивает» мозг, либо укрепляя существующие связи, либо формируя новые нейронные цепочки.
Влияние музыки на обучение
Развитие ребенка через музыки идет по многим направлениям, например:
- Развитие перцептивных и языковых навыков;
- Интеллектуальной развитие;
- Увеличение внимания и концентрации;
- Физическое развитие и здоровье;
- Социальная адаптация и эмоциональное развитие.
Также не стоит забывать, что игра на музыкальных инструментах всегда приводит к повышению самооценки.
Музыка как средство развития ребенка в раннем возрасте
Слушать или заниматься музыкой в любом возрасте полезно. Тем не менее, эксперты считают, что максимальные преимущества достигаются, когда музыкальное обучение начинается в возрасте до семи лет.
Сейчас даже доступны наушники для живота, поэтому мамы могут позволить своему ребенку начать слушать музыку еще до его рождения.
Частота звука или звуковысотность
Представим себе гитару: самая толстая струна натянута не сильно, щипая ее звук получается низким, похожим на жужжание шмеля. А если мы щипнем самую тонкую струну, которая натянута гораздо сильнее, звук получится высоким, похожим на писк комара. Чем чаще колеблется тело издающее звук, тем выше будет этот звук. В данном случае телом можно назвать любой предмет, издающий звук – будь то струна балалайки или мембрана барабана.
Высота звука в физике называется частотой и измеряется в герцах (количество колебаний в секунду). Частота звука в музыке называется звуковысотностью. Ни один музыкант на свете не поймет, какую высоту звука передает нота, если она не располагается на нотном стане. Подробнее о том, как на пяти линейках нотного стана уживаются звуки самой разной высоты, читайте здесь.
Слайды и текст этой презентации
ЛадаНаучный руководитель: Кихтенко Инна Сафроновна

между математикой и музыкой.Найти общие элементы в математике и музыке.Показать,
что построение музыкального произведения имеет свою логику и числовые характеристики (на примерах изучения нотных записей Гимна Российской Федерации и Гимна лицея ТМОЛ).Переложить числа (даты рождения одноклассников) на музыку.Установить связь между консонансным или диссонансным звучанием и способностями личности.Сформулировать выводы.

Слайд 4Актуальность темы состоит в том, что многие не понимают, что
математика и музыка родственны
Родители не принимают во внимание тот. факт, что музыкальное образование развивает способности к математике
Учитывая, что математика становится всё более популярным, но остаётся при этом не менее сложным предметом, ценность музыки и музыкального образования как вспомогательного должна повышаться
факт, что музыкальное образование развивает способности к математике. Учитывая, что математика становится всё более популярным, но остаётся при этом не менее сложным предметом, ценность музыки и музыкального образования как вспомогательного должна повышаться.
АКТУАЛЬНОСТЬ


Слайд 6Одним из первых, кто попытался выразить красоту музыки с помощью
чисел был древнегреческий ученый Пифагор. Он являлся не только знаменитым
математиком, но и блестящим музыкантом. Пифагорейцы видели ключ к разгадке гармонии в познании количественных отношений. Математику и музыку они не разделяли, считая единой наукой о гармонии мира (называли её математой).

Слайд 7Формула консонансаВажную роль в понимании связи между математикой и музыкой
имеет открытие Пифагора. Оно состоит в том, что сочетание звуков,
издаваемых струнами, наиболее благозвучно, если длины струн музыкального инструмента относятся как целые числа первой четверки: 1:2; 2:3; 3:4.Чем ближе в этих отношениях числа к единице, тем более благозвучнее сочетание. Так, самое «красивое» звучание – у октавы, где соотношение частот 1:2.Благозвучное сочетание называется КОНСОНАНС.

Слайд 8Интервалы в музыке и математикеВ математике и музыке много общих
понятий. В основе теории о математике и музыке лежит интервал.
В музыке интервал — расстояние между двумя звуками, которое измеряется тонами и полутонами. Существуют основные интервалы между звуками: Прима – 1 Секунда – 2 Терция – 3 Кварта – 4 Квинта – 5 Секста – 6 Септима – 7 Октава – 8


в начале произведения.1/2 + 1/4 = 1/8 + 1/8 +
1/4 + 1/4 = 1/2 + 1/8 + 1/8 = 3/42) 1/2 + 1/4 + 1/4 = 1 = 1/8 + 1/8 + 1/4 + 1/2 =4/4

0,0000100001… = 0,(00001)Ритм в музыке – чередование длительностей; ритм в
математике – чередование цифр.

Слайд 12Числовые соотношения в нотной записи гимна российской федерацииВывод: сумма
цифр в каждом такте является четным числом. Это
показывает, что мелодия гимна определяется числовыми закономерностями.

Слайд 13Числовые соотношения в нотной записи гимна лицея тмол Вывод:
в данной мелодии идет чередование четных и нечетных сумм цифр
в тактах, что также указывает на подчинение музыки численным законам.

звучание – человек творческий.Диссонансное звучание – человек точен.

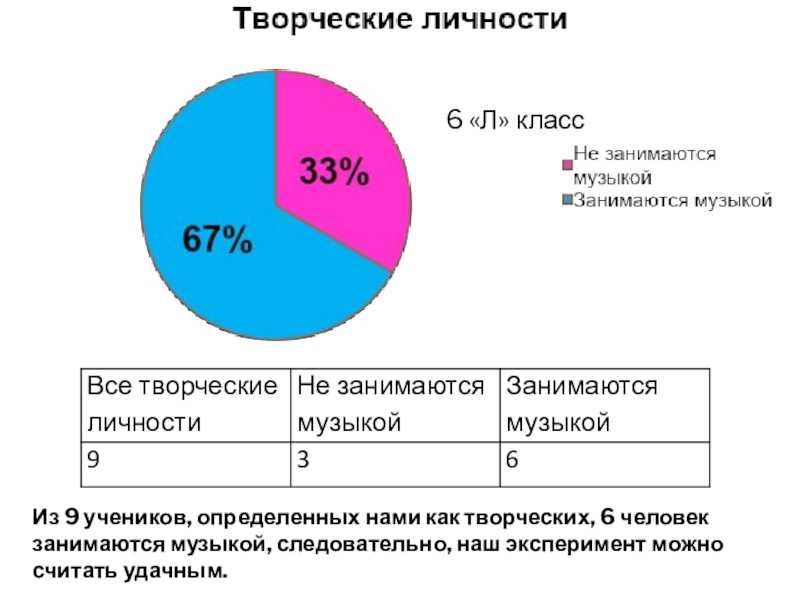
и музыкальными понятиями.Анализ музыкальных произведений (Гимна Российской Федерации и Гимна лицея ТМОЛ) показал, что в их основе лежат численные закономерности.Переложение дат рождения одноклассников на музыку выявило взаимосвязь между консонансным или диссонансным звучанием и способностями личности, что подтвердилось в ходе опроса. Таким образом можно сделать вывод, что между музыкой и математикой существует тесная взаимосвязь, определяющая единство мира чисел и чувств. Цель работы достигнута.

Математический синтез и математический анализ музыки
Этот контакт проявляется при постановке и решении двух основных проблем: математического анализа и математического синтеза музыки. В чем заключаются эти проблемы? Каково их отношение к традиционному, нематематическому музыкознанию?
Музыковедение всегда видело одну из своих основных задач в исследовании, в анализе музыки — с точки зрения мелодики, гармонии, ритмики, формы, инструментовки. Наша первая проблема состоит в использовании для этой цели различных математических дисциплин — статистики, теории информации, теории групп. Оговоримся сразу же: математический анализ музыки и традиционный анализ музыкальных произведений не исключают друг друга. Наоборот, для математического анализа музыки всегда в каком-то объеме необходим предварительный «нематематический» анализ. Результаты же математического анализа не противоречат результатам традиционного анализа, а уточняют их.
Другая основная задача теории музыки с давних пор заключается в ее педагогической функции. Будущий композитор обучается теории музыки, начиная с нотной грамоты, за которой следует учение о гармонии, о музыкальных формах и т д. Проблема математического синтеза музыки вполне аналогична этой задаче, с той «лишь» разницей, что обучать сочинению следует не человека, а машину. Как читатель догадывается, слово «лишь» в предыдущую фразу вставлено в ироническом смысле. В том-то и дело, что человек не машина (точнее, наоборот: современные машины не человек)!
Ведь будущий композитор — обладатель человеческой психики, самого сложного продукта материи. Благодаря этому разные советы и правила он схватывает «на лету», даже если они сформулированы не совсем точно. Пользуясь своим личным вкусом, ученик может оценить, хорошо или плохо звучит музыка, несмотря на то, что он, как правило, не в состоянии объяснить, какими признаками или формальными критериями он при этом руководствовался. Наконец, в его распоряжении фантазия — неиссякаемый источник новых музыкальных идей. Воистину не мудрено из такого великолепного материала сделать композитора! Но попробуйте сделать композитора из вычислительной машины, которая, правда, всему может научиться, но сама не знает ничего.
Даже наиболее элементарные вещи машине требуется сообщать точно и подробно, ничего для нее не подразумевается само собой. Никакого вкуса у нее нет, ибо нет музыкального опыта. И уж совершенно безнадежно выглядит дело с машинной фантазией. Откуда ей взяться?
После всего сказанного у читателя законно возникает вопрос: зачем тогда вообще стараться при помощи машин отнимать хлеб у композиторов-людей? Похоже, что дело это невозможное, да, собственно, и ненужное. Ответим со всей определенностью: никто при помощи «машинной музыки» не собирается превратить композиторов в безработных. Цель серьезных экспериментов по машинному сочинению состоит в другом, и эта цель упомянутыми выше трудностями не снимается, а становится еще более привлекательной. К последнему утверждению мы еще вернемся несколько позже. Теперь, не углубляясь в проблематику анализа, рассмотрим несколько более подробно вопросы, связанные с математическим синтезом музыки.
Но, прежде всего, следует отметить одно обстоятельство, о котором неспециалисты часто забывают. В нашей проблеме речь не идет о конструировании какой-то новой машины неизвестного до сих пор типа, которая будет способна к сочинению музыки. Такие машины уже построены и существуют во многих тысячах экземпляров. Ибо для этой цели пригодна любая универсальная электронная вычислительная машина. Весь вопрос состоит в том, как научиться составить такую последовательность инструкций, такую программу, следуя которой машина сочинит музыку. Итак, выражения «машина может» или «машина не умеет», по существу, следует читать «программа может» или «программа не умеет». Но программу составляет не машина, а человек, поэтому от него, в конечном счете и зависит успех или неуспех машины. Однако читатель ни в коем случае не должен думать, что программист заложил в машину разные мелодии и потом заставил машину эти же мелодии «сочинить». На самом деле автор программы сам не знает, что сочинит машина. Как же в таком случае происходит процесс синтеза? Как преодолеваются упомянутые выше трудности на этом пути?
Обертон или тембр
Очень интересным свойством звука является обертон.
Обертоны – призвуки, входящие в спектр музыкального звука. В переводе с немецкого языка, обертон означает «высокий тон» или «высокий звук». А откуда берется этот высокий звук, сейчас и узнаем.
Струна колеблется целиком, вы сами это видели на видео про гитару. Но оказывается, каждая часть струны тоже вибрирует и издает звук. Не такой громкий как основной тон, но вполне ощутимый.
Еще Пифагор определил принцип, по которому возникают обертоны. Он заключается в следующем:
Первый обертон возникает от вибрации половины звучащего тела – в нашем случае струны. То есть, если мы зажмем струну в том месте, где она делится пополам, то звук получится в два раза выше, чем звук полной струны. Это и есть звучание первого обертона. Но чтобы услышать его в чистом виде, нужно использовать специальный прием – флажолет.
Теперь поделим струну на 3 равные части. Одна треть струны даст нам второй обертон. Затем делим струну на 4 части, получаем третий обертон и так далее.
Вот как выглядит колебание струны: 1 – Целая струна; 2 — ее половина – первый обертон; 3 — третья часть – второй обертон и т.д.
Посмотрите, как с помощью флажолетов можно извлечь обертона:
Пифагор установил, что первый обертон звучит выше основного тона на одну октаву. Второй обертон звучит выше первого на квинту; третий – выше второго на кварту; четвертый выше третьего на большую терцию. Потом пойдут малые терции, затем большие и малые секунды. Вот как выглядит обертоновый ряд от ноты до:
Именно от набора и относительной громкости обертонов зависит тембр инструмента, голоса. Именно благодаря тембру, мы можем отличать звук флейты от звука арфы, звук рояля от звука трубы.































