Как научить ребенка считать в уме

Уроки устного счета

Уроки устного счета, представленные в нашем курсе, направлены именно на развитие трех вышеназванных составляющих. Вот их краткое описание:

Урок 1

Внимание и концентрация. Чтобы научиться считать в уме по-настоящему быстро, необходимо уметь концентрироваться на конкретном примере

Этот навык полезен не только для совершения математических операций, но и для решения любых жизненных задач. Умение быть внимательным в нужный момент – этот навык, который выделяет великих ученых, спортсменов, политиков, несомненно, пригодится и вам

Чтобы научиться считать в уме по-настоящему быстро, необходимо уметь концентрироваться на конкретном примере. Этот навык полезен не только для совершения математических операций, но и для решения любых жизненных задач. Умение быть внимательным в нужный момент – этот навык, который выделяет великих ученых, спортсменов, политиков, несомненно, пригодится и вам.

Урок 2. Простые арифметические закономерности

Чтобы уметь решать сложные арифметические задачи, нужно для начала усвоить некоторые базовые закономерности. От того, как быстро вы сможете считать простейшие примеры, напрямую зависит ваше умение быстро выполнять более сложные математические операции. По сути, это можно считать базой для всего последующего обучения.

Урок 3. Традиционное умножение в уме

В этом уроке мы рассмотрим, как можно умножать двузначные числа, используя традиционные методы, которым нас обучают в школе. Некоторые из этих методов могут позволить вам быстро перемножать в уме двузначные числа при достаточной тренировке

Знать эти методы полезно, однако важно понимать, что это лишь вершина айсберга. В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел

Урок 4. Частные методики умножения двузначных чисел до 30

Способы умножения двузначных чисел хороши тем, что они универсальны для любых чисел, и при хорошем навыке могут позволить вам достаточно быстро прийти к правильному ответу. Однако эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов. В этом уроке вы узнаете, как можно быстро умножать любые числа до 30. Здесь представлены специальные методики, в том числе и введение в использование опорного числа.

Урок 5. Опорное число при умножении чисел до 100

Наиболее популярной методикой умножения больших чисел в уме является прием использования так называемого опорного числа. Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. При умножении чисел до 100 опорными числами удобно использовать все числа кратные 10, а особенно 10, 20, 50 и 100. В уроке вы познакомитесь с данной методикой и научитесь сами ее применять.

Урок 6. Умножение в уме любых чисел до 100

Чтобы умножать любые числа до 100 в уме, важно быстро подобрать нужный алгоритм. Для удобства этого подбора в данном уроке выделены наиболее эффективные случаи для каждой методики умножения

В уроке будут рассмотрены как универсальные методики (подходящие для любых чисел), так и частные (удобные для конкретных случаев).

Урок 7. Возведение в квадрат в уме

Умение считать в уме квадраты чисел может пригодиться в разных жизненных ситуациях, например, для быстрой оценки инвестиционных сделок, для подсчета площадей и объемов, а также во многих других случаях. Кроме того, умение считать квадраты в уме может служить демонстрацией ваших интеллектуальных способностей. В этом уроке разобраны методики и алгоритмы, позволяющие научиться этому навыку.

Также в нашем курсе представлены дополнительные материалы, помогающие тренировать и развивать умение считать устно:

Книги, учебники и ссылки на материалы по устному счету

К сожалению, в Интернете далеко не всегда удается найти качественные материалы, посвященные именно обучению счету в уме. Однако есть ряд интересных книг и сайтов, связанных с вопросами устного счета. С некоторыми из них вы и сможете познакомиться поближе, изучив данный раздел.

Дополнительные материалы по устному счету

Уместить в один курс всю важную и нужную информацию очень проблематично. Но она, несомненно, нужна, так что вы сможете углубить свои знания по рассматриваемой теме. В этом разделе вы найдете небольшую подборку полезных материалов (а именно эффективных обучающих программ и статей), которые помогут вам лучше изучить отдельные вопросы.

Далее предлагаем познакомиться с краткой инструкцией по прохождению курса.

Как быстро и легко выучить таблицу умножения с ребёнком?

Рассмотрим несколько, проверенных личным опытом, практических советов, которые, при применении на практике, дают очень хороший результат.

Совет №1

Большую роль в усвоении таблицы умножения играет понимание смысла умножения. Объясните ребёнку смысл действия умножения и научите этим пользоваться при вычислениях.

Умножение – это сумма одинаковых слагаемых.

8 умножить на 3 – это значит, что число 8 мы должны взять 3 раза: 8 х 3 = 8 + 8 + 8

Понимая смысл умножения, ребёнок сможет найти результат даже в ситуации, когда он забыл какой-то случай из таблицы.

Например, забыв результат умножения числа 4 на 8, можно заменить умножение сложением и найти произведение: 4 х 8 = 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32.

Важно знать переместительное свойство умножения (от перестановки множителей произведение не меняется), тогда результат можно найти ещё быстрее: 4 х 8 = 8 х 4 = 8 + 8 + 8 + 8 = 32

Умножать можно с помощью рук

Умножение на 9

Для этого положите руки ладонями вверх, пальцы разогните. Мысленно пронумеруйте пальцы слева направо от 1 до 10. Загните тот палец, на какое число нужно умножить 9. Например, нужно 9х3. Загибаете 3 палец. Все пальцы слева (их 2 — это десятки), пальцы справа (их 7) — единицы. Соединяем десятки и единицы, получаем — 27.

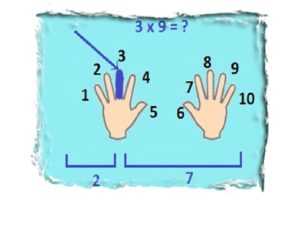
Вычисление произведения любых однозначных чисел больше, чем 5

Способ 1

Пронумеруйте мысленно пальцы на обеих руках. Мизинец — 6, безымянный — 7, средний — 8, указательный — 9, большой — 10 (на то он и БОЛЬШОЙ, чтобы выражать самое БОЛЬШОЕ число).

Допустим, вы хотите узнать, сколько будет 8 х 7. Соедините вместе средний палец левой руки (8) с безымянным правой (7), как показано на рисунке. А теперь считайте. Два соединённых пальца плюс те, что под ними, указывают на количество десятков в произведении. В данном случае — 5. Число пальцев, оказавшихся над одним из сомкнутых пальцев, умножьте другим сомкнутым пальцем. В нашем случае 2 х 3 = 6. Это — число единиц в искомом произведении. Десятки складываем с единицами, и ответ готов — 56.

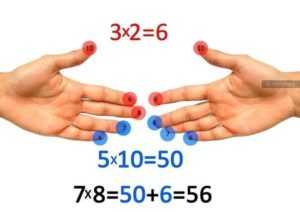
Способ 2

Например, нужно умножить 7х7. Загнём на левой руке столько пальцев, на сколько первый множитель больше 5, а на правой руке столько пальцев, на сколько второй множитель больше 5.

В данном случае будет загнуто по 2 пальца. Если сложить количество загнутых пальцев и перемножить количество не загнутых, то получится соответственно число десятков и единиц искомого произведения, т.е. 49. Если этим способом вычислять произведение 6х7, то получится 3 десятка и 12 единиц, т.е. 30+12=42

Проверьте и убедитесь, что эти способы действительно работают.

Совет № 3

Знание правил умножения упростит запоминание таблицы умножения:

При умножении любого числа на 1 получается то число, которое умножали.
Все результаты умножения на 10 начинаются с числа, которое мы умножаем, а заканчиваются на 0.
Все результаты умножения на 5 заканчиваются на 5 или 0: если умножали нечётное число – на 5, если чётное – на 0.
Чтобы умножать на 4, можно просто дважды удваивать число. Например, чтобы умножить 6 на 4, нужно удвоить 6 два раза: 6 + 6 = 12, 12 + 12 = 24.
При умножении на 9, запишите ряд ответов в столбик: 09, 18, 27, 36, 45, 54, 63, 72, 81, 90. Запомнить нужно первое и последнее число. Все остальные можно воспроизвести по правилу: первая цифра в двузначном числе увеличивается на 1, а вторая уменьшается на 1.

Научиться пользоваться таблицей Пифагора

Необходимо показать ребёнку, что числа из левого столбика умножаются на числа из верхней строки. Найти результат очень просто: нужно только провести рукой по таблице вниз и вправо от множителей до места пересечения, где и будет расположен результат умножения.

Возьмите пустую распечатанную или нарисованную таблицу и заполните её вместе с ребёнком. Причем в цвете, закрашивая одинаковый результат одним цветом. Сразу будет видна закономерность. Ребёнок увидит, что запоминать нужно только половину таблицы (согласно переместительному закону умножения).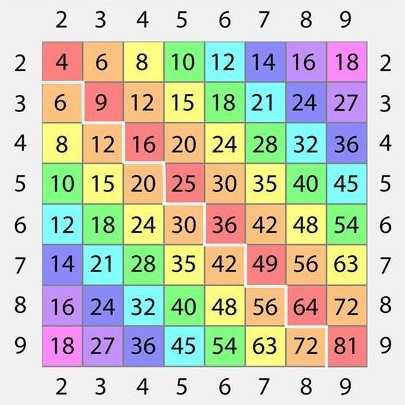

Понимая смысл умножения, можно использовать для вычислений предыдущие или последующие табличные случаи. При этом случае нужно лишь вычесть или прибавить нужное число.

Действие умножения

Если понимать, что умножение – это сложение одинаковых чисел определенное количество раз, ничего сложного в действии нет. Например, 4*7 = 4+4+4+4+4+4+4. В итоге получают 28. Упростит действие таблица умножения. Ее знает каждый школьник.

Чтобы правильно умножать числа, их сводят к простым. Рассмотрим техники умножения.

Умножение 9 и 11

Правило при умножении на 9 умножают на 10 и вычитают 9. Если умножают на 11, сначала умножают на 10, прибавляя исходный показатель.

Пример:

15*9 = 15*10-15 = 150-15 = 135;
57*11 = 57*10+57 = 570+57 = 627.

Умножение на 5 чисел до 10

Эта техника поможет правильно умножать двух-, трехзначные числа. Правило простое – множитель делят на 2. Получив результат в виде целого показателя, добавляют в конце 0, а если число не целое, отбрасывают остаток и добавляют в конце 5.

Пример 1482*5 решают так:

(1482/2) _ (+0 или +5) = 741 _ (+0) = 7410 – исходный показатель делили на 2 без остатка;
2269-5 = (2269/2) _ (+0 или +5) = 1134,5 _ (+5) = 11345 – исходный показатель делили на 2 с остатком.

Техника, как быстро научиться считать деньги, умножая число на 5, 25, 50, 125 с использованием формул:

А*5 = А*10/2;
А*50 = А*100/2;
А*25 = А*100/4;
А*125 = А*1000/8.

Приставляя вместо А цифру, в процессе решения формулы получают нужный результат. Например, 25*25 = 25*100/4 = 2500/4 = 625.

Умножение больших чисел с одним четным

В этом случае пользуются методикой упрощения множителей. Четное число уменьшают в 2 раза, а нечетное увеличивают в 2 раза. Например, 48*125 = 24*250 = 12*500 = 6*1000 = 6000.

Умножение многозначного числа на однозначное

Разбираясь, как научиться быстро считать деньги на кассе, пользуются техникой раскладывания на порядки, как в случае сложения. Пример 468*6 решают так:

Раскладывают 468 на 400, 60, 8. Умножают каждое число на 6.
Получают (400*6) = 2400 + (60*6) = 360 + (8*6) = 48. Итого 2400+360+48 = 2808.

Более сложный вариант с перегруппировкой итоговых результатов выглядит так: 2400+360+48 = 2000+400+300+60+48 = 2000+700+108 = 2808.

Умножение простых чисел

Диагональный метод нужен при поисках техники как быстро научиться считать устно. Заключается способ в дописывании числа, которого «не хватает до 10».

Пример 7*8 решают так:

высчитают недостающее до 10 – в 7 это 3, в 8 это 2;
затем 8-3 = 5;
3*2 = 6;
в итоге получают 56.

Умножение чисел от 10 до 20

Правило – к одному числу прибавляют единицы другого, а сумму умножают 10. К результату добавляют сумму единиц. Например, 13*15 = (13+5)*10 + 3*5 = 180+15 = 195.

Умножение двузначных чисел

Упрощают процесс снова разложением двузначных чисел на простые действия. Пример 78*56 решают так:

В итоге должно получиться сложение цифры 78 точно 56 раз. Сначала складывают 78 пятьдесят раз, затем еще 6 раз.
Считают 78*5 = 70*5 + 8*5 = 350+40 = 390*10 = 3900.
78*6 = 70*6 + 8*6 = 420+48 = 468.
3900+468 = 3000+900+400+60+8 = (3000+1300+60+8) = 4368.

Пользуясь принципом упрощения и раскладывания больших чисел на разряды, умножают все двузначные числа.

Умножение на 9, 99, 999

Учитывают правило прибавления недостающих единиц. Пример 154*99 решают так: 154*(100-1) = 15400-154 = 15246. Таким же образом умножают на 9, 999.

Возведение в квадрат

Это тоже умножение, при котором число раскладывают на составляющие. Сначала находят произведение первой цифры на следующую за ней, результат будет заканчиваться на квадрат последней цифры. Пример возведения 75 в квадрат решают так: 7*8 = 56; 5*5 = 25. В итоге 75*75 = 5625.

С чего и когда начинать?

Начинать обучение устному счету возможно уже в 2 – 3 года, постепенно усложняя задачи. Главное при этом – считать в процессе игры. Например, собирая кубики или пирамидки, проговаривать: «Кладем первый кубик (первое кольцо), сверху – второй. Смотри, кубик был один, теперь их стало 2».

В игровой форме у ребенка просыпается естественный интерес– и он учится легко. При этом нужно помнить, что ребенок младшего дошкольного возраста запоминает лишь то, что ему интересно. Игра для этого будет лучшим способом. Главное здесь – расположение и поддержка родителей, их умение заинтересовать кроху процессом. А за этим придет нужный результат.

В 3–4 года можно считать кнопки, застегивая куртку, количество ложечек каши, которые малыш скушал на завтрак, число тарелок или ложек на столе, число ступенек до двери подъезда и т. д. На прогулке можно считать машины (если считать только красные или белые, можно заодно закрепить и название цветов), кошечек или фонари. Можно в магазине посчитать, сколько куплено яблок, йогуртов или еще чего-то штучного, во время готовки – количество продуктов, которые берет мама.

Визуализации счета способствуют и карточки с изображением количества предметов и числовых обозначений. Играя с ними, можно научить ребенка понимать, например, что цифра 3 – это 3 яблока. То есть малыш научится соотносить количество и его числовое изображение. Такие карточки можно сделать самостоятельно и применять начиная с 4 лет.

С помощью карточек, развивающих пособий или игрушек можно объяснять ребенку состав числа. То есть, что 5 зайчиков можно получить, если сложить 2 и 3, 1 и 4, или 3+2, 4+1. При этом слагаемые поменялись местами, но результат остался прежним. Это необходимо, чтобы научить ребенка решать простые примеры. Кстати, складывать или вычитать в пределах десяти дети прекрасно учатся на обычных монетах. Например, считая, сколько нужно монет, чтобы купить конфету. В 5–6 лет дошкольник с удовольствием будет складывать цифры на номерах машин (скажем, 135 – это 1+3+5).

Еще один способ закрепить это понимание (а также соотношения больше-меньше, один-много) – игра в магазин. Ребенок назначается продавцом. На столе раскладывают «товары» (фрукты, овощи, игрушки, книжки), присваивая каждому из них карточку-ценник с обозначением конкретного числа. Например, яблоко стоит 2 монетки (можно придумать свое название денежной валюты – будет только интереснее). Затем малыш должен будет считать покупки мамы, вычислять, сколько денег они стоят.

Мама может сказать: «У меня 3 яблока. Груш мне нужно на 1 меньше». Или: «Я беру 2 йогурта. Мне нужно, чтобы йогуртов и печенья было поровну». Можно развивать эту игру так, как подскажет фантазия родителей, задавая самые разнообразные вопросы, изучая не только счет, но и простейшие вычисления. Главное – чтобы чаду было интересно считать.

Как быстро и легко выучить таблицу умножения: лучшие способы

Вот несколько простых для понимания и отлично работающих способов для изучения таблицы умножения вместе с ребёнком:

Таблица Пифагора

Классическая для российского образования схема таблицы умножения может испугать объёмом — выходит, что школьнику придётся учить целых сто примеров.

Замените привычную таблицу таблицей Пифагора, и вместо 100 арифметических действий останется запомнить всего 36.

Как освоить умножение с помощью таблицы Пифагора:

1. Сделайте таблицу Пифагора, в которой будут указаны только множители.

2. Вместе с ребёнком заполните пустые клетки. Со многими примерами младший школьник справится самостоятельно. Расскажите, что достаточно сложить 2 и 2, и дальше к каждой полученной сумме прибавлять 2: 2 + 2 = 4, 4 + 2 = 6, 6 + 2 = 8 и т.д.

Таким же способом заполните клетки с остальными множителями: 3 + 3 = 6, 6 + 3 = 9; 4 + 4 = 8, 8 + 4 = 12, и т.д.

Обратите внимание ребёнка на то, что, аналогично принципу сложения, в умножении от перемены множителей результат не меняется: например, если умножать числа 4 на 6 или 6 на 4 — получается 24 в обоих случаях

4. Помогите сыну или дочери прийти к выводу, что почти половина примеров повторяется, только множители меняются местами – остаётся запомнить 55 примеров вместо 100.

5. Подскажите другие закономерности, которые не нужно заучивать:

число, умноженное на единицу, остаётся равным самому себе;
при умножении на 10 достаточно дописать к числу 0, чтобы получить правильный ответ (2 х 10 = 20, 3 х 10 = 30 и т.д.).

Благодаря изучению таблицы умножения с помощью таблицы Пифагора ребёнку останется выучить всего 36 примеров вместо ста.

Карточки умножения

Можно использовать готовые карточки или сделать их самостоятельно — так ребёнок начнёт запоминать таблицу сразу в процессе подготовки карточек.

Как выучить таблицу с помощью карточек:

От простого к сложному

Дети легче запоминают таблицу, когда учат примеры не подряд, а переходят от простых к более трудным. Попробуйте выучить умножение в таком порядке:

единицы и десятки: самые простые примеры, с которыми обычно проблем не возникает (число, помноженное на 1, остаётся прежним; к умноженному на 10 добавляется 0);
на 5: при умножении чётного числа на 5 обязательно получится чётное число, оканчивающееся на ноль (2 х 5 = 10, 4 х 5 = 20), при умножении нечётного числа на 5 получится нечётное число, оканчивающееся на 5 (7 х 5 = 35, 9 х 5 = 45);
на 2 и на 4: умножение на 2 — это всегда одно и то же число, сложенное с собой (2 х 2 = 4, 3 х 2 = 6); на 4 — то же, что и умножение на 2, но увеличенное в два раза, то есть можно умножить число на 2 и прибавить к нему то же самое число (2 х 4 = 2 х 2 + 4 = 8);
на 9. Проще всего запомнить с помощью пальцев:
1. пусть ребёнок повернёт ладони вверх и мысленно даст пальцам номера от 1 до 10, считая слева направо (начиная с большого пальца левой руки),
2. попросите ребёнка загнуть тот палец по счёту, который соответствует цифре, умножаемой на 9,
3. например, при умножении 3 на 9 нужно загнуть третий слева палец, оставшиеся разогнутыми два пальца слева — это десятки, семь пальцев справа — единицы, в итоге получается 3 х 9 = 27;
на 3, 6, 7, 8: можно выучить наизусть или подключить другие способы – карточки, плакаты, рифмы, настольные игры, попробовать учить на пальцах.

Какие методики использовать для быстрого счета в уме

Многими методами устного счета вполне можно овладеть самостоятельно. Главное – выбрать хорошую методику, заниматься регулярно и не останавливаться при возникновении трудностей. Далее мы рассмотрим несколько методик, которые показали себя с лучшей стороны при обучении детей разного возраста.

Умножение на 10

Одна из наиболее простых методик для устного счета. В таком случае нужно умножить любое число на 10, а потом вычесть из него то же самое число.

Простые пример: 19*10-19= 190-19=171.

Таким образом можно быстро считать большинство примеров. Более того, ребенок, понимания принципы работы счета, сможет лучше понять, как работает математика

Это важно, чтобы не сформировать с раннего возраста боязнь предмета в силу его предполагаемой сложности

Умножение на 11

Еще один похожий вариант – умножение на 11. Представим, что нам нужно решить пример 67*11. Как быть в такой ситуации? Используем следующую последовательность действий: 67*10+67=670+67=737. И так можно поступать с любыми примерами и числами, ответ будет правильный.

Умножение двузначного числа на однозначное

Метод также можно использовать в качестве удобного математического тренажера для мозга. Нам нужно будет разобрать имеющиеся множители на единицы и десятки. Рассмотрим на примере 56*8.

Сначала нам нужно взять число 56 и разделить его на десятки и единицы. Получится 50 и 6.

Полученное нужно умножать отдельно по следующему принципу: 50*8+6*8=400+48=448.

Мы рекомендуем переходить к такому методу только после того, как два предыдущих уже были хорошо освоены. При этом нужно двигаться от простого к сложному, постепенно брать все более и более крупные числа.

Умножение двузначного числа на двузначное

Методики быстрого счета в уме для детей часто полагаются на этот способ. Он предполагает, что нужно будет умножать двухзначные числа и во многом напоминает метод, который мы описывали ранее.

Для примера возьмем умножение 24*52. Для этого нам снова нужно будет разделить эти числа на единицы и десятки, а потом уже перемножить непосредственно на множитель. Пример в таком случае решается следующим образом: 20*52+4*52=1040+208=1248.

Сложность примеров во время занятий также нужно постепенно увеличивать, чтобы не тормозить свой прогресс.

Высчитывание процентов

Хорошо показывает себя на практике и методика поиска процентов от числа, с которым приходится работать. Чтобы это сделать, требуется умножить число на процент, который из него предполагается выделить и полученное разделить на 100.

Этот метод пригодится и взрослым, потому что он помогает перепроверить проценты при оформлении кредита или внесении платежей по различным услугам.

Деление многозначного числа на однозначное

Отличным способом становится также деление многозначного числа на однозначное. Этот способ опирается на хорошее понимание таблицы умножения, потому будет полезен для желающих освежить математические знания в любом возрасте.

Представим, что нам поставлена задача поделить 138 на 6. Первым делом уже привычно разделяем делимое число на десятки и единицы. У нас будет 13 десятков и 8 единиц.

Полученное нужно делить на 6. Также если мы делим 13 на 6, получается 2 и 1 в остатке. Таким образом мы получаем понимание, что в ответе десятком будет число 2. Остаток нужно будет сложить с единицами. В нашем случае остатком становится число 10. Выполняем действие 10+8 и получаем ответ – 18.

Нам остается поделить 18 на 6. Ответ будет равен 3. Далее мы складываем полученные ответы – три и два десятка. Ответом получаем 23.

Если рассматривать все описанное в виде примера, у нас получится следующее: 120/6+(10+8)/6=20+18/6=23.

5 правил обучения счета

Не знаете, как быстро научить ребенка различать цифры и устно считать? Следуйте правилам:

Регулируйте объем изучаемого материала. Занятия должны быть ежедневными, продолжительность каждого – не более 10 минут. Лучше разделить обучение на 3 подхода. В идеале – утром, в обед и вечером. Так ребенок не будет уставать из-за изобилия новой информации, не потеряет интерес к занятиям.
Не увлекайтесь. Пройденный материал лучше вспоминать лишь тогда, когда действительно нужно. Пытаться объяснять счет, пока ребенок кушает или занимается личной гигиеной, глупо.
Не давайте слишком сложные задания. Не стоит ругать и наказывать ребенка, если у него что-то не получается. Чтобы получить действительно положительный результат, нужно начинать с малого. Подбирайте малышу те задачи, с которыми он точно сможет справиться.
Закрепляйте пройденный материал. Помните, дети хорошо запоминают информацию в процессе игры. Чаще занимайтесь с ними подсчетом всего, что находится рядом: чашки на столе, птички на проводе, автомобили на парковке.
Соблюдайте порядок. Психологи считают, что процесс освоения новой информации состоит из трех последовательных этапов: привыкание, понимание и запоминание.

Наберитесь терпения

Устно считать – важно и нужно, однако не следует торопить ребенка. Результат появится очень быстро, если вы создадите условия комфортного общения, будете поддерживать и оказывать всестороннюю помощь малышу

Особенности вычитания

В математике существует всего два «полноправных» действия — сложение и умножение. Вычитание и деление являются обратными от этих двух. Кроме того, их всегда можно заменить умножением, подставив число «x», или сложением, подставив знак минус к неизвестному слагаемому. Именно поэтому, чтобы научиться вычитанию, сперва необходимо научиться складывать числа. Ведь в любой момент можно просто поменять в уме переменные и проверить правильность решения с помощью «x». Методика вычитания трехзначных чисел практически ничем не отличается от сложения. Вот небольшой пример: 553−192, а также подробный разбор:

Разбить имеющиеся числа на сотни, десятки и единицы: 500=500+50+3, 192=100+90+2.
Провести вычитание с сотнями: 500−100=400.
Вычесть десятки, заняв одну сотню: 150−90=60.
Вычесть единицы: 3−2=1.
Сложить остатки, не забыв о заемных сотнях или десятках: «300+60+1=361».

То есть даже в вычитании будет обязательно присутствовать сложение. Основная сложность расчета таких примеров заключается в постоянной необходимости занимать десятки. Однако если проводить такую тренировку ежедневно, то со временем считать трехзначные числа будет ненамного сложнее, чем двухзначные. Самое главное — верить в себя и собственные силы.

https://youtube.com/watch?v=prss6ysMGJY

Способы быстрого счета

Существует определенный набор простейших арифметических правил и закономерностей, которые не только нужно знать для устного счета, но и постоянно держать в голове, чтобы в нужный момент оперативно применить самый эффективный алгоритм. Для этого необходимо довести их использование до автоматизма, закрепить в машинальной памяти, чтобы от решения самых простых примеров успешно перейти к более сложным арифметическим действиям. Вот основные алгоритмы, которые нужно знать, помнить и применять мгновенно, автоматически:

Вычитание 7, 8, 9

Чтобы вычесть 9 из любого числа, нужно вычесть из него 10 и прибавить 1. Чтобы вычесть 8 из любого числа, нужно вычесть из него 10 и прибавить 2. Чтобы вычесть 7 из любого числа, нужно вычесть из него 10 и прибавить 3. Если обычно вы считаете по-другому, то для лучшего результата вам нужно привыкнуть к этому новому способу.

Быстро умножить любое число на 9 можно при помощи пальцев рук.

Деление и умножение на 4 и 8

Деление (или умножение) на 4 и на 8 являются двукратным или трехкратным делением (или умножением) на 2. Производить эти операции удобно последовательно.

Например, 46*4=46*2*2 =92*2= 184.

Умножение на 5

Умножать на 5 очень просто. Умножение на 5, и деление на 2 – это практически одно и то же. Так 88*5=440, а 88/2=44, поэтому всегда умножайте на 5, поделив число на 2 и умножив его на 10.

Умножение на однозначные числа

Чтобы быстро считать в уме, полезно уметь умножать двузначные и трехзначные числа на однозначные. Для этого нужно умножать двух- или трехзначное число поразрядно.

Например, умножим 83*7.

Для этого сначала умножим 8 на 7 (и допишем ноль, так как 8 – разряд десятков), и прибавим к этому числу произведение 3 и 7. Таким образом, 83*7=80*7 +3*7= 560+21=581.

Возьмем более сложный пример: 236*3.

Итак, умножаем сложное число на 3 по разрядно: 200*3+30*3+6*3=600+90+18=708.

Определение диапазонов

Чтобы не запутаться в алгоритмах и по ошибке не выдать совсем неверный ответ, важно уметь строить примерный диапазон ответов. Так умножение однозначных чисел друг на друга может дать результат не более 90 (9*9=81), двузначных – не более 10 000 (99*99=9801), трехзначных не более – 1 000 000 (999*999=998001)

Раскладка на десятки и единицы

Способ заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.

Например:

63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 +3*5=4800+300+240+15=5355

Проще такие примеры решаются в 3 действия:

1. Сначала умножаются десятки друг на друга. 2. Потом складываются 2 произведения единиц на десятки. 3. Затем прибавляется произведение единиц.

Схематично это можно описать так:

– Первое действие: 60*80 = 4800 – запоминаем – Второе действие: 60*5+3*80 = 540 – запоминаем – Третье действие: (4800+540)+3*5= 5355 – ответ

Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты

Мысленная визуализация умножения в столбик

56*67 – посчитаем в столбик. Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа.

Но его можно упростить: Первое действие: 56*7 = 350+42=392 Второе действие: 56*6=300+36=336 (ну или 392-56) Третье действие: 336*10+392=3360+392=3 752