Когда появились цифры и кто их первым придумал

Слайды и текст этой презентации

Слайд 1МБОУ «Анциферовская основная общеобразовательная школа»
Манина Р.М.Из истории чисел«Числа правят миром»

Слайд 21. Числа начинают получать именаОДИН — происходит от латинского слова

«солюс» ДВА — связано с предметами встречающимися попарно (крыльями, ушами

и т. д.)

А иногда их связывали с местоимениями «Я» и «Ты», были языки, где «один» звучало так же, как «мужчина» а «два»— как « женщина».

Слайд 3ТРИ – сначала применяли вместо слова «много»И сейчас мать, рассердившись

на непослушного сына, говорит ему: «Что я, три раза должна

повторять одно и то же!»

А во многих сказках герой сражается с трехглавым змеем,в других сказках проходит три царства — медное, серебряное и золотое.

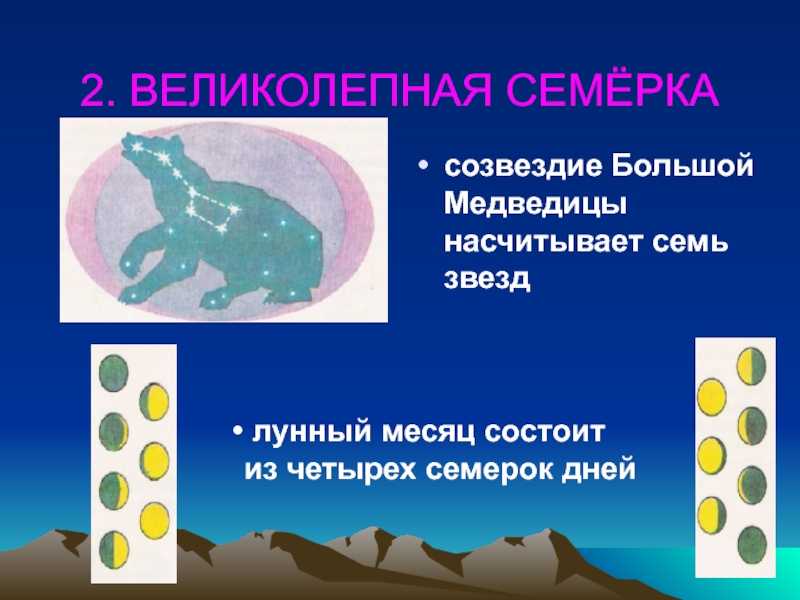
Солнце, Луна) Да и сейчас мы пользуемся семидневной неделей и

говорим о семи цветах радуги

Слайд 63. ЖИВАЯ СЧЁТНАЯ МАШИНАПальцы это прекрасная вычислительная машина!!! С их

помощью можно считать до 5, используядве руки — до 10,

а с ногами легко считать до 20.

На древнегреческом языке считать — «пятерить»А в русском языке слово « пять», это «пясть» — часть руки

Слайд 74. СОРОК И ШЕСТЬДЕСЯТ Следующим за десятью узловым числомстало у

одних народов число 40, а у других — число 60

«Сорок медведей поддел на рогатину -На сорок первом сплошал!» (Н.А. Некрасов стихотворение «В деревне»)

В старой системе мер: в пуде считалось 40 фунтов, в бочке — 40 ведер и т. д

Слайд 8 До сих пор мы делим час на 60 минут,

а минуту на 60 секунд. Окружность делят на 360,

то есть 6х60 градусов, градус — на 60 минут, а минуту — на 6О секунд.

Как моряки в древности вели корабль от одного острова к другому, так и в «числовом море» выделялись острова,то есть узловые числа —10, 40, 60, 100.

Слайд 9ПословицыЗа двумя зайцами погонишься, ни одного не поймаешь.Двое пашут, а

один глаз зорок — не надобно сорок.

5.ЧИСЛА ВОКРУГ НАС

шесть. И спешат к нему старушки сушек Сашиных поесть.

Слайд 11Поэзия Час

обеда приближался, Топот по двору

раздался: Входят семь богатырей, Семь румяных усачей.

«Сказка о мертвой царевне и семи богатырях»

Три девицы под окном пряли поздно вечерком.

«Сказка о царе Салтане»

Слайд 13 В третий раз закинул невод, пришел невод

Слайд 14«Сказка о попе и его работнике Балде»Живет Балда в поповом

доме, Спит себе на соломе,Ест за четверых,Работает за семерых…С первого

щелчка прыгнул поп до потолка; Со второго щелчка лишился поп языка, А с третьего щелчка вышибло ум у старика.

Сказки

у меняДва серебряных коня. Езжу сразу на обоих. Что за

кони у меня? (коньки)

Слайд 20Вывод: Невозможно представить современную жизнь без чисел,

Древние римляне: пятёрки и десятки

На первый взгляд, древние римляне так же, как греки, пользовались алфавитной записью чисел. На самом деле, они использовали только некоторые буквы для условного обозначения единиц и пятёрок в десятеричных разрядах. К слову, изначально часть этих цифробукв к буквам отношения не имели, это были похожие на римские буквы этрусские значки, условно обозначающие палец (I  – единица), ладонь (V – пятёрка, только у этрусков она была углом кверху) и две ладони рядом (X – десять). Римляне также пользовались для обозначения чисел буквами L (50, пять десятков), C (100), D (500, пять сотен) и M (1000). Большие числа обозначали, ставя наверху буквы черту, означавшую умножение на 1000. Так, 5000 – это V (5) с чертой, 10 000 – X (10) с чертой, и так далее. 2015 год древний римлянин обозначил бы вот так: MMXV (1000+1000+10+5). При таком способе записей отдельная буквоцифра для нуля не нужна, так что и самого нуля как числа римляне не знали.

Математика в древней Греции

Древнегреческие математики сделали значительное вклад в развитие математики в целом. Важным достижением была разработка геометрии, которую они начали изучать уже в V веке до н.э. Геометрия, основанная на аксиомах и доказательствах, стала одним из важнейших разделов математики.

Крупнейшими представителями древнегреческой математики были Пифагор, Евклид и Архимед.

Пифагор, основатель пифагорейской школы, положил начало изучению чисел, их свойств и взаимосвязей. Он обнаружил важные законы в математике, например, теорему Пифагора, которая гласит, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Это открытие стало основой для дальнейшего развития геометрии и алгебры.

Евклид, автор знаменитой «Начал геометрии», сформулировал аксиоматический подход к изучению геометрии. Он описал геометрические фигуры и доказал множество основных теорем, которые сегодня известны под именем теорем Евклида.

Архимед сделал большой вклад в математику и физику. Он разработал новые методы вычислений площадей и объемов фигур, придумал способы приближенного вычисления числа Пи и сформулировал закон Архимеда о всплытии тел в жидкости.

В целом, математика в древней Греции была важным элементом философии и науки того времени. Она помогала древним грекам понять и объяснить многие явления, а также совершать точные измерения и вычисления.

Весёлые картинки древних египтян

У соплеменников Тутанхамона и Нефертити было очень развитое иероглифическое письмо – того требовала не менее развитая бюрократия, однако и они не стали выделять отдельных значков под цифры. Единица обозначалась тем же иероглифом, что черта, десятка – пяткой, сотня – петлёй верёвки, тысяча – лотосом. А вот десять тысяч для европейца особенно неожиданны, потому что именно эту часть тела мы ассоциируем с жалкими единицами – палец! Сто тысяч обозначались жабой, а вот значок миллиона был уникальным. Он изображал мужчину, преклонившего колено и поднявшего руки, как бы в потрясении перед таким числом. Хотя, если вдуматься, миллион – это ведь всего лишь сто жаб или тысяча пальцев.

Сложные числа обозначались просто: значок единицы, десятка, сотни и так далее повторялся нужное количество раз, поэтому некоторые числа выглядят утомительно длинными. Да, нуля египтяне тоже не знали, но, в отличие от греков, справлялись с вычислениями как-нибудь так. С другой стороны, им было намного легче: ведь проще сложить три пальца две пятки и жабу пять лотосов, расставив их в нужном порядке вместе, чем НБ (ню бета) с ТОД (тау омикрон дельта).

Америка.[]

Исследователи, путешествовавшие в 16 в. по Центральной Америке, обнаружили цивилизации с высокоразвитыми системами счисления, отличными от тех, которые были известны в Европе. Самыми важными элементами в системе счисления майя были использование позиционного принципа и символа нуля. Если отвлечься от того, что принятая у индейцев майя система счисления была не шестидесятиричной, а двадцатиричной и вместо 10 использовала вспомогательное основание 5, то в остальном принципы были аналогичны тем, которые ранее были в ходу у жителей Древнего Вавилона. В схеме майя точка означала единицу, а повторяющиеся точки – числа до четырех; пятерку обозначала горизонтальная черта, а две и три горизонтальные черты обозначали, соответственно, числа десять и пятнадцать. Для обозначения числа двадцать майя воспользовались позиционным принципом, используя точку, помещенную над символом нуля. (Последний имел вид .)

Числа в системе счисления древних майя записывались в столбец, причем верхние символы были старшими. Самая нижняя позиция соответствовала разряду единиц; «этажом выше» располагалось число двадцаток. Еще выше единица соответствовала не кратным числа 400, как можно было бы ожидать, а кратным числа 360. За исключением этого разряда, связанного, насколько можно судить, с календарными соображениями и продолжительностью года, все остальные более высокие позиции соответствовали степеням числа 20. Число 6789 в системе счисления, принятой у майя, записывалось как

Система счисления у ацтеков в Мексике была более последовательно двадцатиричной, чем у майя, но в остальном менее тонкой, так как не использовала ни позиционный принцип, ни специальный символ для нуля. Точка означала у ацтеков единицу, а для обозначения степеней числа 20 были введены новые знаки: флаг для 20, дерево для 4

00 и кошелек для 8000. При необходимости другие числа представлялись с помощью повторения этих символов, а от их чрезмерного повторения они избавлялись, вводя специальные промежуточные коллективные знаки: ромбовидный знак для 10 и фрагменты дерева для 100, 200 или 300.

До появления в Северной Америке европейцев индейцы не имели письменности. Исследования древних систем счисления показывают, что используемые названия чисел были в основном прилагательными и лишь в отдельных случаях достигали уровня абстракции, когда они становились существительными. Тем не менее с помощью рисунков или устно индейцы могли выразить число вплоть до миллиона. Системы составления чисел были самыми различными, но примерно половина из них по существу была десятичной.

Способы счета в древнем Египте

В древнем Египте люди использовали особые методы для счета, которые отличались от того, что мы используем сегодня. Они разработали свою систему численности, основанную на десятичной системе.

Основными символами в системе счета древних египтян были гирины, символизирующие единицы, и ситоты, которые обозначали десятки. Гирины представлялись в виде вертикальных черт, а ситоты — в виде знака для десяти ситот — горизонтальной черты.

Использование такой системы позволяло древним египтянам считать большие числа. Они могли комбинировать различные символы, чтобы получить нужное число. Например, число 25 можно было представить с помощью двух гирин и пяти ситот, что выглядело как IIIIIIIIIIIIIIIIIII_____.

Кроме основных символов, существовали и другие знаки, которые обозначали другие числа. Например, знак, похожий на нашу запятую, обозначал число 1/2, а знак, похожий на корзину, обозначал число 3/4.

Древние египтяне также использовали систему относительного счета, основанную на использовании знаков для разных единиц. Например, символ для 1000 обозначался фигурой лотоса, а символ для 10000 — фигурой стрелы. Это позволяло им считать даже очень большие числа.

Система счета в древнем Египте была весьма сложной. Она требовала обширных знаний и большой концентрации при счете. Однако, благодаря этой системе, древние египтяне смогли развиться в многих отраслях, включая математику и астрономию.

Римская система счета и арифметика

Основные символы римской системы счета:

• I — 1
• V — 5
• X — 10
• L — 50
• C — 100
• D — 500
• M — 1000

Римская арифметика была основана на комбинировании этих символов. Например, чтобы представить число 4, нужно использовать символы IV, а для представления числа 9 — символы IX.

Основные правила римской системы счета:

1. Символы могут быть записаны в любом порядке, но при их сложении следует соблюдать убывающий порядок (от большего к меньшему).
2. Если меньший символ предшествует большему, их значения складываются (например, IV = 4).
3. Если меньший символ следует за большим, его значение вычитается из значения большего символа (например, CM = 900).

Римская система счета использовалась в Римской империи и продолжала применяться в Европе вплоть до средневековья. В наше время она остается интересной исторической особенностью математики.

Индийские цифры и система нумерации

Индийские цифры имеют следующие символы:

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9

Каждый из этих символов олицетворяет определенное число. Например, символ «3» означает число «три».

Индийская система нумерации основана на позиционной системе, в которой каждая позиция в числе имеет вес, связанный с ее расположением от младшей к старшей позиции. Это позволяет представлять числа любой величины, используя всего 10 символов.

Индийские цифры стали популярными в Европе только в XII веке н.э. во время изучения арабских математических текстов, в которых использовались эти символы. К числу преимуществ индийских цифр относится их простота использования, а также понятность и эффективность для математических операций.

Индия.[]

Письменных памятников древнеиндийской цивилизации сохранилось очень немного, но, судя по всему, индийские системы счисления проходили в своем развитии те же этапы, что и во всех прочих цивилизациях. На древних надписях из Мохенджо-Даро вертикальная черточка в записи чисел повторяется до тринадцати раз, а группировка символов напоминает ту, которая знакома нам по египетским иероглифическим надписям. В течение некоторого времени имела хождение система счисления, очень напоминающая аттическую, в которой для обозначения чисел 4, 10, 20 и 100 использовались повторения коллективных символов. Эта система, которая называется кхарошти, постепенно уступила место другой, известной под названием брахми, где буквами алфавита обозначались единицы (начиная с четырех), десятки, сотни и тысячи. Переход от кхарошти к брахми происходил в те годы, когда в Греции, вскоре после вторжения в Индию Александра Македонского, ионическая система счисления вытеснила аттическую.

Вполне возможно, что переход от кхарошти к брахми происходил под влиянием греков, но сейчас вряд ли возможно хоть как-то проследить или восстановить этот переход от древних индийских форм к системе, от которой произошли наши системы счисления. Надписи, найденные в Нана-Гат и Насике, относящиеся к первым векам до нашей эры и первым векам нашей эры, по-видимому, содержат обозначения чисел, которые были прямыми предшественниками тех, которые получили теперь название индо-арабской системы. Первоначально в этой системе не было ни позиционного принципа, ни символа нуля. Оба эти элементы вошли в индийскую систему к 8–9 вв. вместе с обозначениями деванагари (см. таблицу обозначений чисел). Здесь мы впервые встречаемся с элементами современной системы счисления: индийская система была десятичной, цифровой и позиционной. При желании можно даже усмотреть некоторое сходство в начертании современных цифр и цифр деванагари.

Напомним, что позиционная система счисления с нулем возникла не в Индии, поскольку за много веков до этого она использовалась в Древнем Вавилоне в связи с шестидесятиричной системой. Поскольку индийские астрономы использовали шестидесятиричные дроби, вполне возможно, что это навело их на мысль перенести позиционный принцип с шестидесятиричных дробей на целые числа, записанные в десятичной системе. В итоге произошел сдвиг, приведший к современной системе счисления. Не исключена также возможность, что такой переход, по крайней мере отчасти, произошел в Греции, скорее всего в Александрии, и оттуда распространился в Индию. В пользу последнего предположения свидетельствует сходство кружка, обозначающего нуль, с начертанием греческой буквы омикрон. Однако происхождение индийского символа для нуля окутано тайной, так как первое достоверное свидетельство его появления в Индии датируется лишь концом 9 в. Как ни странно, ни греки, ни индийцы не включили в свои системы счисления десятичные дроби, но именно индийцам мы обязаны современной системой записи обыкновенных дробей с числителем, расположенным над знаменателем (но без горизонтальной черты, отделяющей числитель от знаменателя).

Инки: узелки на память

У инков было два типа письменности. Классическая, узелками (“кипу”) и двумерная, в виде записей на пергаменте, листьях и даже орнаментов на одежде (“килька”). Кипу имела несколько видов сложности. Числовой записью узелками владели все взрослые инки. Простым письмом владели образованные люди (например, чиновники – инки были очень бюрократической империей), и письмом сложным, необходимым для подробных и детальных записей – только учёные и хронисты. Килька по умолчанию считалась элитным видом письменности, простым людям запрещено было ею пользоваться. Числа, как и слова, в кипу обозначались узелками определённой формы. Учёные утверждают, что инки пользовались десятеричной системой счисления и записывали числа, как мы показываем их на счётах – только вместо рядов костяшек были ряды узлов. Надо сказать, европейские цифры инки выучивали от испанцев на раз, находили их такими простыми, что аж скучно и глупо, и откровенно высмеивали. В ответ оскорблённые испанцы занимались систематическим уничтожением кипу. Так пропали многие бесценные исторические хроники. К слову, инки были первым народом, который использовал двойной счёт в бухгалтерии (записывали дебет с кредитом). Для вычислений они использовали специфический вид счёт, юпану. Некоторые современные учёные полагают, что юпана работала на фибоначчиевой системе счисления, изобретённой инками, конечно же, задолго до Фибоначчи.

Древний Египет.[]

Расшифровка системы счисления, созданной в Египте во времена первой династии (ок. 2850 до н.э.), была существенно облегчена тем, что иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах. Из этих надписей нам известно, что древние египтяне использовали только десятичную систему счисления. Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. Чтобы записанные таким образом числа было легко узнавать, вертикальные штрихи иногда объединялись в группы из трех или четырех черт. Для обозначения числа 10, основания системы, египтяне вместо десяти вертикальных черт ввели новый коллективный символ, напоминающий по своим очертаниям подкову или крокетную дужку.
Множество из десяти подковообразных символов, т.е. число 100, они заменили другим новым символом, напоминающим силки; десять силков, т.е. число 1000, египтяне обозначили стилизованным изображением лотоса. Продолжая в том же духе, египтяне обозначили десять лотосов согнутым пальцем, десять согнутых пальцев – волнистой линией и десять волнистых линий – фигуркой удивленного человека. В итоге древние египтяне могли представлять числа до миллиона.
Самые древние из дошедших до нас математических записей высечены на камне, но наиболее важные свидетельства древнеегипетской математической деятельности запечатлены на гораздо более хрупком и недолговечном материале – папирусе. Два таких документа – папирус Ринда, или египетского писца Ахмеса (ок. 1650 до н.э.) и московский папирус, или папирус Голенищева (ок. 1850 до н.э.) – служат для нас основными источниками сведений о древнеегипетских арифметике и геометрии. В этих папирусах более древнее иероглифическое письмо уступило место скорописному иератическому письму, и это изменение сопровождалось использованием нового принципа обозначения чисел. Иероглифическая запись чисел использовалась преимущественно в официальных документах и текстах. Еще позднее иератическая система обозначения чисел уступила место демотическим системам записи.
Введение египтянами цифровых обозначений ознаменовало один из важных этапов в развитии систем счисления, так как дало возможность существенно сократить записи. Однако их операции с дробями продолжали оставаться на примитивном уровне, так как они знали лишь аликвотные дроби (т.е. дроби с числителем 1) и каждую дробь записывали в виде суммы аликвотных дробей, например, дробь 2/43 они записали бы так: 1/42 + 1/86 + 1/129 + 1/301. В этих системах счисления над символом, обозначающим знаменатель, ставился специальный знак. В искусстве оперирования дробями египтяне значительно уступали жителям Месопотамии

История древних способов счета

С появлением цивилизаций у людей возникла необходимость считать и учета. Древние цивилизации разработали различные способы подсчета, которые впоследствии эволюционировали и привели к появлению современной математики.

Один из самых древних способов счета — пальцы рук. Люди использовали пять пальцев на каждой руке, чтобы отслеживать количество. Этот метод применяется по сей день во многих культурах.

Другим распространенным способом подсчета было использование гравированных камней или паличек. Люди могли добавлять или удалять камни или палички для отслеживания чисел. Этот метод использовался в древних цивилизациях, таких как Месопотамия и Древний Египет.

Древние цивилизации также разработали системы счисления, которые основывались на основании 10. Одна из самых известных таких систем — десятичная система счисления, которая используется по сей день. Другие цивилизации, такие, как Майя и Бабулонцы, разработали свои собственные системы счисления.

Кроме того, некоторые древние цивилизации использовали способы подсчета, основанные на геометрических фигурах. Например, Древний Египет использовал систему счета, основанную на единицах измерения, таких как пядь или локоть.

История древних способов счета показывает, что люди сотни и тысячи лет назад имели потребность в точном и эффективном подсчете. Это потребность привела к разработке различных систем счета, которые дали начало современной математике, которую мы используем сегодня.

Китай.[]

Одна из древнейших систем счисления была создана в Китае, а также в Японии. Эта система возникла как результат оперирования с палочками, выкладываемыми для счета на стол или доску. Числа от единицы до пяти обозначались, соответственно, одной, двумя и т.д. палочками, выкладываемыми вертикально, а одна, две, три или четыре вертикальные палочки, над которыми помещалась одна поперечная палочка, означали числа шесть, семь, восемь и девять. Первые пять кратных числа 10 обозначались одной, двумя, пятью горизонтальными палочками, а одна, две, три и четыре горизонтальные палочки, к которым сверху приставлялась вертикальная палочка, означали числа 60, 70, 80 и 90. Для обозначения чисел больше 99 использовался позиционный принцип. Число 6789 китайцы записали бы так: . Обозначения чисел с помощью палочек тесно связано со счетом на пальцах и счетной доске, но применялось оно также и в письменных вычислениях.

Во второй китайской системе счисления для обозначения первых девяти целых чисел или символов используют девять различных знаков и одиннадцать дополнительных символов для обозначения первых одиннадцати степеней числа 10. В сочетании с умножением и вычитанием это позволяло записывать любое число меньше триллиона. Если один из символов, обозначающих первые девять целых чисел, стоит перед (при чтении слева направо) символом, означающим степень числа 10, то первое нужно умножить на второе, если же символ одного из девяти первых целых чисел стоит на последнем месте, то это число надлежит прибавить к обозначенному предыдущими символами.

Смайлики от майя

А вот у майя было целых два способа записывать цифры. Наверное, для скучных людей и для весёлых. В системе для скучных ноль записывался ракушкой, единица – точкой, пятёрка – линией, и этих трёх значков хватало для обозначения любого числа. Тем более, что записывались числа примерно по тому же принципу, что у нас, только система была не десятеричной, а двадцатеричной. То есть, запись точка и ракушка (10) означала наши двадцать (20). А настоящая десять записывалась как две черты (5 и 5).

Второй способ записывать числа – иероглифы в виде голов, каждая из которых обозначает числа от 0 до 19. Причём эта система была наполовину десятеричной: начиная с 11, голова имеет чёткую приставную челюсть, как у 10.

Очевидно, для вычислений использовался первый тип записи, как более наглядный, а головоцифры были только для каллиграфии по камню. Почти как с греками, только возле майя не было своих вавилонцев, чьи цифры можно было бы использовать для математических операций, и им пришлось стать самим себе вавилонцами.